Question

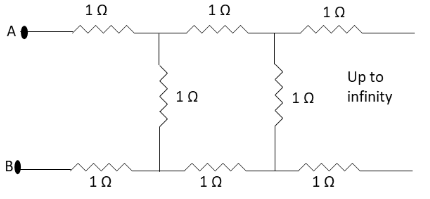
The resistance between the terminal point A and B of the given infinitely circuit will be:

A. \[\left( {\sqrt 3 - 1} \right)\]
B. \[\left( {1 - \sqrt 3 } \right)\]
C. \[\left( {1 + \sqrt 3 } \right)\]
D. \[\left( {2 + \sqrt 3 } \right)\]

Answer 1

Hint: First consider a resistance R as the net resistance in the branches of the circuit including the terminals A and B. Redraw the given circuit diagram according to this. Calculate the equivalent resistance between the resistances R and \[1\,\Omega \] connected in parallel and then lastly calculate the equivalent resistance of all resistances connected in parallel.

Formulae used:
The equivalent resistance \[{R_{eq}}\] of the two resistors \[{R_1}\] and \[{R_2}\] connected in series is
\[{R_{eq}} = {R_1} + {R_2}\]
The equivalent resistance \[{R_{eq}}\] of the two resistors \[{R_1}\] and \[{R_2}\] connected in parallel is
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\]

Complete step by step answer:
Let us readraw the give circuit diagram as below:

In the above circuit diagram, R is the equivalent resistance of all the resistance connected in series in the branch containing terminals A and B and one resistance \[1\,\Omega \] in the branch connecting the two branches of terminals A and B.

The resistance R and \[1\,\Omega \] in the above diagram are parallel to each other. The equivalent resistance of these two resistances in parallel is
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{R} + \dfrac{1}{{1\,\Omega }}\]
\[ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{R + 1}}{R}\]
\[ \Rightarrow {R_{eq}} = \dfrac{R}{{R + 1}}\]

Now the remaining two resistances \[1\,\Omega \] of and the resistance \[{R_{eq}}\] are in series with each other. The equivalent resistance of these resistances is \[R\].
\[R = 1\,\Omega + 1\,\Omega + \dfrac{R}{{R + 1}}\]
\[ \Rightarrow R = 2 + \dfrac{R}{{R + 1}}\]
\[ \therefore R = 1 + \sqrt 3 \]
Therefore, the resistance between the terminals A and B of the given circuit is \[1 + \sqrt 3 \].

Hence, the correct option is C.

Note: The students should be careful while determining the net resistance between the various resistors connected in series and parallel. One should first check which resistors are connected in parallel and which are connected in series and then determine the net resistance because if this is done incorrectly then the final value of resistance will also be incorrect.