Question

The respective angles of a flint glass prism and a crown glass prism are $A$ and $A'$ and their refractive indices for the mean ray are given by n and n’ respectively. If these two prisms are to be combined to produce dispersion without deviation of the mean ray, then $\dfrac{A}{A'}$ should be:
A. $\dfrac{n-1}{n'-1}$
B. $-\left( \dfrac{n'-1}{n-1} \right)$
C. $\dfrac{n+1}{n'+1}$
D. $\dfrac{n'+1}{n+1}$

Answer 1

Hint: As per the given question, we can understand that the sum of deviation caused by the prism combination is zero, in other words, deviation caused by one is the negative of that caused by another. We could now express the deviations of the prisms in terms of their respective prism angles and then equate the relation for one of the prisms as the negative of the other. Rearranging the terms will now lead you to the required ratio.

Formula used: $\delta =\left( \mu -1 \right)A$

Complete step by step answer:
We know very well that, when a white light is incident on a glass prism, it gets dispersed into its constituent colors. This happens because light with different wavelengths are getting bend in varying amounts.

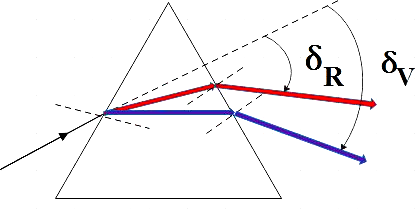
${{\delta }_{v}}$, ${{\delta }_{R}}$ are the deviations that has occurred for red light and violet light from the path that it would have followed in the absence of the prism.
So we are given two glass prisms - flint glass prism and crown glass prism, and they are arranged in such a way that resultant deviation caused by them is zero.

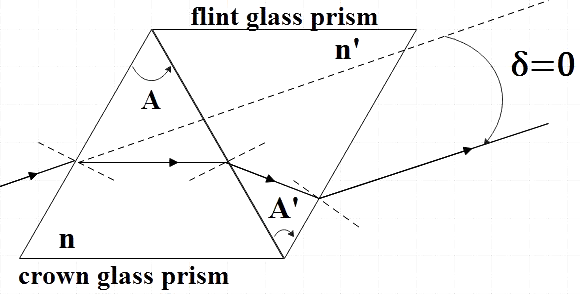
The ray represented in this diagram is the mean ray. The light incident on the surface of flint glass prism is bent due to change in refractive index. Let the deviation caused due to the presence of flint glass prism be${{\delta }_{f}}$. The light is further bent when it hits the flint–crown interface and let the deviation caused due to crown glass prism alone be $\delta c$.
We are provided in the question that this arrangement results in dispersion without deviation. Therefore, the sum of deviations of both glass prisms should be zero. That is,
${{\delta }_{total}}={{\delta }_{f}}+{{\delta }_{c}}=0$
Clearly,
 ${{\delta }_{f}}=-{{\delta }_{c}}$ …………………….. (1)
The relation between the angle of prism and the deviation caused by it is given by,
$\delta =\left( \mu -1 \right)A$ …………………. (2)
Where, μ is the refractive index of the prism.
We are given n and n’ as the refractive indices of flint glass and crown glass, also, A and A’ as their respective angles of prism.
Equation (2) for flint glass and crown glass are,
${{\delta }_{f}}=\left( n-1 \right)A$ ………………. (3)
${{\delta }_{c}}=\left( n'-1 \right)A'$ ……………… (4)
Substituting (3) and (4) in (1) gives,
$\left( n-1 \right)A=-\left( n'-1 \right)A'$
Therefore,
$\dfrac{A}{A'}=-\left( \dfrac{n'-1}{n-1} \right)$

So, the correct answer is “Option B”.

Note: Here, the deviation caused by one prism is negative of the other, thereby resulting in zero deviation. Though deviation is absent, we could still observe dispersed light at the end of this arrangement. Absence of deviation just means that, at the end, the light traces the path that is parallel to the one it would have taken in the absence of this arrangement.