Question

The resultant magnetic moment for the following arrangement is (the vectors are non-coplanar)

A) M
B) 2M
C) 3M
D) 4M

Answer 1

Hint : The magnetic moment vectors add up directly when they are in the same direction. Calculate the next magnetic moment due to vectors that are in the same direction and then add them to find the net magnetic moment of the vectors that are oriented at an angle to each other

Formula used:
$ |\vec R| = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $ where $\vec R$ is the resultant t vector formed by the addition of vectors P and Q that have an angle $\theta $ between them.

Complete step by step answer
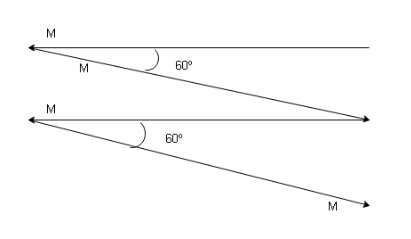
The magnetic moments for the arrangement given in the question can be condensed into the addition of two vectors since the vectors that are in the same direction will add up directly as shown below

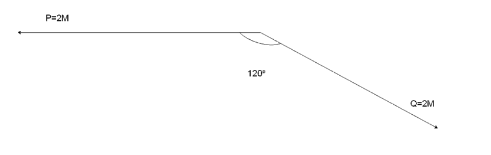
Now the resultant vector of the addition of vectors P and Q, since they’re not in the direction, can be calculated using the formula
$ |\vec R| = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $
Placing the value of $P = 2M$ and $Q = 2M$ the angle between them as $120^\circ $ we can calculate the magnitude of the resultant vector as
$ |\vec R| = \sqrt {4{M^2} + 4{M^2} + 2(4{M^2})\cos 120^\circ } $
$ |\vec R| = \sqrt {8{M^2} + 8{M^2}\left( { - \dfrac{1}{2}} \right)} $
On simplifying, we can get
$ |\vec R| = \sqrt {4{M^2}} $
$ |\vec R| = 2M$
So, the net resultant magnetic moment of the configuration given in the question will be 2M which corresponds to option (B)

Note
Since the vectors in the same direction add up directly, we don’t have to add up all 4 vectors individually and we only have to use the vector addition formula to the resultant two vectors. The magnitude of the resultant vectors must be calculated taking into account the angle between the two vectors, i.e. the angle formed between the tails of the two vectors which is $120^\circ $ and not $60^\circ $.