Answer
Verified469.8k+ views
Hint: We can draw a regular hexagon and its circumcircle and incircle. Then we can draw the radius of both the circles to the center. We can form a right-angled triangle and form trigonometric ratios between the radius of both circles. Thus we get the required ratio by giving the angle to the trigonometric function.
Complete step by step answer:
We can draw a regular hexagon and its circumcircle an incircle.
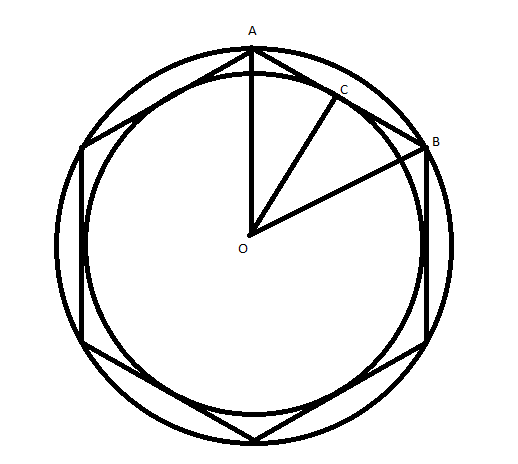
From the figure, we have OA is the radius of the circumcircle and OC is the radius of the incircle.
We know that each angle of a regular hexagon is $120^\circ $. Then AO is also an angle bisector of the hexagon.
So we get, $\angle OAC = 60^\circ $
As AB is a tangent to the incircle through C , OC is perpendicular to AB
Now consider right-triangle AOC,
$\sin \theta = \dfrac{{opp.{\text{ }}side}}{{hypotenuse}}$
$\sin \angle OAC = \dfrac{{OC}}{{OA}}$
Substituting the value of the angle, we get,
$\sin {60^0} = \dfrac{{OC}}{{OA}}$
We know that $\sin {60^0} = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \dfrac{{OC}}{{OA}} = \dfrac{{\sqrt 3 }}{2}$
The required ratio is OA to OC. So we can take the reciprocal.
$ \Rightarrow \dfrac{{OA}}{{OC}} = \dfrac{2}{{\sqrt 3 }}$
Therefore the required ratio is$\dfrac{2}{{\sqrt 3 }}$.
So the correct answer is option D.
Note: Hexagon is polynomial having 6 sides. For a regular polygon, all the angles will be equal and all the sides will be equal. The circumcircle is the circle that passes through all the vertex of a polygon. Its centre is called the circumcentre. In the circle is the circle inscribed on a polygon or the circle that touches all the sides of the polygon. Its centre is called in the centre. For a hexagon sum of the interior angles is $720^\circ $and for a regular hexagon, each angle will be$120^\circ $. While taking the ratio, the order is important. While taking the sin of the angle, we will get the reciprocal of the required ration. We take its reciprocal to get the required ratio.
Complete step by step answer:
We can draw a regular hexagon and its circumcircle an incircle.
From the figure, we have OA is the radius of the circumcircle and OC is the radius of the incircle.
We know that each angle of a regular hexagon is $120^\circ $. Then AO is also an angle bisector of the hexagon.
So we get, $\angle OAC = 60^\circ $
As AB is a tangent to the incircle through C , OC is perpendicular to AB
Now consider right-triangle AOC,
$\sin \theta = \dfrac{{opp.{\text{ }}side}}{{hypotenuse}}$
$\sin \angle OAC = \dfrac{{OC}}{{OA}}$
Substituting the value of the angle, we get,
$\sin {60^0} = \dfrac{{OC}}{{OA}}$
We know that $\sin {60^0} = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \dfrac{{OC}}{{OA}} = \dfrac{{\sqrt 3 }}{2}$
The required ratio is OA to OC. So we can take the reciprocal.
$ \Rightarrow \dfrac{{OA}}{{OC}} = \dfrac{2}{{\sqrt 3 }}$
Therefore the required ratio is$\dfrac{2}{{\sqrt 3 }}$.
So the correct answer is option D.
Note: Hexagon is polynomial having 6 sides. For a regular polygon, all the angles will be equal and all the sides will be equal. The circumcircle is the circle that passes through all the vertex of a polygon. Its centre is called the circumcentre. In the circle is the circle inscribed on a polygon or the circle that touches all the sides of the polygon. Its centre is called in the centre. For a hexagon sum of the interior angles is $720^\circ $and for a regular hexagon, each angle will be$120^\circ $. While taking the ratio, the order is important. While taking the sin of the angle, we will get the reciprocal of the required ration. We take its reciprocal to get the required ratio.