Question

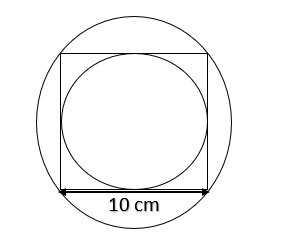
The side of a square is 10 cm. Find the area between the inscribed and circumscribed circle of the square.

Answer 1

Hint: Use the information, for inscribed circle: radius $ = \dfrac{{{\text{side of square}}}}{2} \Rightarrow {r_1} = \dfrac{{10}}{2} = 5cm$ and for circumscribed circle: diameter of the circle = diagonal of the square. Also, the area between these circles is nothing but the difference of their area.

Complete step-by-step answer:

For inscribed circle: radius$ = \dfrac{{{\text{side of square}}}}{2} \Rightarrow {r_1} = \dfrac{{10}}{2} = 5cm$.
We know that, area of the circle is given by $\pi {r^2}$.
So, the area of the inscribed circle is $\pi {r_1}^2 = \pi \times {5^2} = 25\pi c{m^2}$.
For circumscribed circle: diameter of the circle = diagonal of the square.
We can use Pythagoras theorem to find the length of the diagonal of the square.
${(diagonal)^2} = {10^2} + {10^2} = 2 \times 100 \Rightarrow diagonal = 10\sqrt 2 cm$.
Then, radius $ = \dfrac{{diagonal}}{2} \Rightarrow {r_2} = \dfrac{{10\sqrt 2 }}{2} = 5\sqrt 2 cm$.
 Now, again we can use the formula of area of the circle for circumscribed circle which is $\pi {r_2}^2 = \pi \times {(5\sqrt 2 )^2} = 50\pi c{m^2}$.
Now, the area between these circles is nothing but the difference of their area which is $50\pi - 25\pi = 25\pi c{m^2} \approx 78.511c{m^2}$.

Note: It’s preferable, not to put the value of $\pi $ in the middle of the solution. It’ll create complex calculations which we don’t want. Better to put the value in the final answer as we did in this solution.