Question

The side of a square is equal in length to the diameter of a circle, which figure will have the greater area?

Answer 1

Hint: Here in this question, we have to find the greater area between the square and circle having its same length of side and diameter. For this, we have to consider the formula of area of circle $$A = \pi {r^2}$$, where ‘$$r$$’ be the radius of circle which equals half of the diameter and area of square $$A = {a^2}$$, where ‘$$a$$ ‘ be the length of the side of square, then on comparing the both formulas and by considering a example we get the required solution.

Complete step by step answer:
A circle is a round shaped figure that has no corners or edges. It is made up of many points arranged equidistant from a single central point and the point is known as the centre of the circle.
Area of a circle is the region occupied by the circle in a two-dimensional plane. It can be determined easily using a formula, $$A = \pi {r^2}$$, (Pi r-squared) where ‘$$r$$’ is the radius of the circle.
A square is a two-dimensional closed shape with 4 equal sides. A square is a quadrilateral. 
Area of a square is the region occupied by the square. It can be determined easily using a formula, $$A = {a^2}$$, ($$sid{e^2}$$) where ‘$$a$$’ length of the side.
Let us consider
Area of circle: $$\pi {r^2}$$ ---- (1)
As we know that, the radius of a circle is half of its diameter i.e., $$r = \dfrac{d}{2}$$
Then equation (1) becomes
$$ \Rightarrow \,\,\pi {\left( {\dfrac{d}{2}} \right)^2}$$
On simplification, we have
$$ \Rightarrow \,\,\,{d^2}\dfrac{\pi }{4}$$ ---- (2)
By Given, if the diameter of a circle is the same as the side length of square, then 
The area of square is: $${d^2}$$ ------ (3)
‘$${d^2}$$’ will always be greater than ‘$${d^2}\dfrac{\pi }{4}$$’.
Since ‘$$4$$’ is always greater than $\pi$.
Example: If the length of the side of the square and diameter of the circle is 4cm.
Area of square: $${a^2}$$
Given, $$a = 4$$
$$ \Rightarrow \,\,A = {4^2}$$
$$\therefore $$ Area of square: $$16$$ cm.
Area of circle: $$\pi {r^2}$$ or $$\,\pi {\left( {\dfrac{d}{2}} \right)^2}$$
Given, $$d = 4$$
$$ \Rightarrow \,\,A = \pi {\left( {\dfrac{4}{2}} \right)^2}$$
$$ \Rightarrow \,\,A = \pi \left( {\dfrac{{16}}{4}} \right)$$
$$ \Rightarrow \,\,A = 4\pi $$
But the value of $$\pi = \dfrac{{22}}{7} = 3.14$$.
$$ \Rightarrow \,\,A = 4\left( {3.14} \right)$$
$$ \Rightarrow \,\,A = 4\left( {3.14} \right)$$
$$\therefore $$ Area of circle: $$12.56$$ cm.
Since, $$16 > 12.56$$.
Therefore, The area of the square will be greater than the area of the circle.
Let’s assume both the square side length and the circle radius are the same length. It’ll look like this:

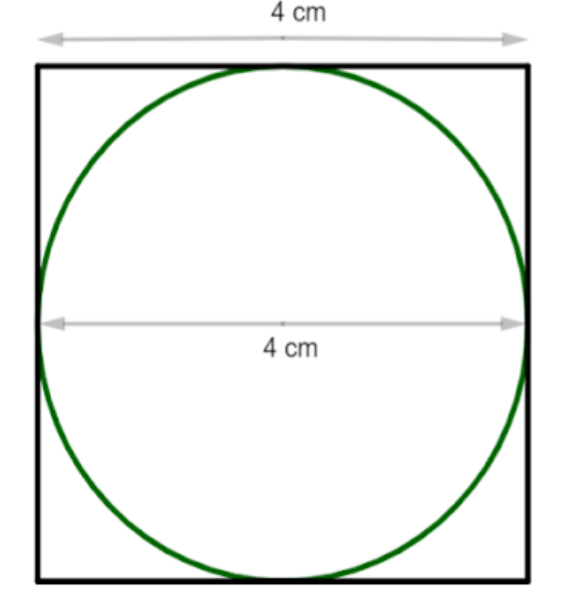
Note:
If the diameter of the circle is known to us, we can calculate the radius of the circle, such as $$r = \dfrac{d}{2}$$. In mensuration problem don’t forget to write the units, The unit of area of both square and circle is the square unit, such as $${m^2}$$, $$c{m^2}$$, etc. and don’t forget the $$\pi $$ or $$pi$$ which is a Greek letter. It is a very important constant in mathematics. Whose value is $$\pi = \dfrac{{22}}{7} = 3.14$$.