Question

The side of the square inscribed in the circle of circumference 220cm is?
A) $ 45cm $
B) $ 48cm $
C) $ 35\sqrt 2 cm $
D) $ 40\sqrt 2 cm $

Answer 1

Hint: By the given circumference we can find the radius of the circle and thus, the diameter. Then the biggest square that can be inscribed in the circle will have the diameter of the circle as its diagonal. Using Pythagoras theorem, we can then find the side of the square.
Formula used-
Formulae used are as follows
Circumference of circle- $ C = 2\pi r $
Pythagoras theorem- $ {H^2} = {P^2} + {B^2} $

Complete step-by-step answer:
First, we can visualize the question using the following diagram. Let the circumference of circle be C and the radius of the given circle be r, therefore, diameter will be 2r. Let the sides of the inscribed square be a.

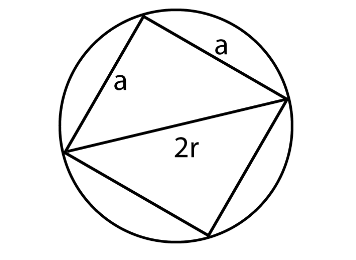
A square that fits snugly inside a circle is inscribed in the circle. The square's corners will touch, but not intersect, the circle's boundary, and the square's diagonal will equal the circle's diameter. Also, as is true of any square's diagonal, it will equal the hypotenuse of a 45°-45°-90° triangle
So, according to the question,
 $ C = 220cm $
We know that,
 $
  C = 2\pi r \\
   \Rightarrow 220 = 2 \times \pi \times r \\
   \Rightarrow r = \dfrac{{220}}{2} \times \dfrac{7}{{22}} \\
   \Rightarrow r = 35cm \;
  $

Radius of the circle is 35cm. As, we can see from the diagram that the biggest square that can be inscribed in the circle will have the circle’s diameter as its diagonal.
Diameter $ = 2r = 2 \times 35cm = 70cm $
Applying Pythagoras theorem on the inscribed square’s one half,
 $
  {\left( {2r} \right)^2} = {a^2} + {a^2} \\
   \Rightarrow {\left( {70} \right)^2} = 2{a^2} \\
   \Rightarrow {a^2} = \dfrac{{{{70}^2}}}{2} \\
   \Rightarrow a = \sqrt {\dfrac{{70 \times 70}}{2}} = 35\sqrt 2 cm \;
  $
Therefore, the side of the square is $ 35\sqrt 2 cm $ and the correct option is C).
So, the correct answer is “Option C”.

Note: The main mistake made by students here is that they assume the inscribed square will have its side equal to the diameter of the circle only, which is to be avoided. Also, The diameter (or diagonal) divides the inscribed square into two right triangles joined hypotenuse-to-hypotenuse. Both the triangles have legs of 4 (since the square has sides of 4) and interior angles of 45°, 45°, and 90°. For either one, you can find the hypotenuse using the trigonometric ratios of triangles too.