Question

The sides of a cyclic quadrilateral are in A.P. The length of the shortest side is 6 and the difference between the longest and the shortest side is also 6. What will be the square of the area of the quadrilateral?

Answer 1

Hint: Draw a rough diagram of a cyclic quadrilateral. Assume the sides of the quadrilateral as a, a + d, a + 2d, and a + 3d starting from shortest to longest respectively. Take the difference of (a + 3d) and ‘a’ and equate it with 6 to find the value of d. Here, ‘a’ is the first term of the A.P. and ‘d’ is a common difference. After finding the length of all the sides, apply the formula for area of a quadrilateral given as: - Area = \[\sqrt{\left( s-a \right)\left( s-b \right)\left( s-c \right)\left( s-d \right)-abcd{{\cos }^{2}}\dfrac{\theta }{2}}\] to get the answer. Here, ‘s’ is the semi-perimeter of the quadrilateral given as: - \[s=\dfrac{a+b+c+d}{2}\], where a, b, c, and d are the four sides of the quadrilateral, and ‘\[\theta \]’ is the sum of opposite angles of the quadrilateral. Use the theorem that “sum of opposite angles of a cyclic quadrilateral is \[{{180}^{\circ }}\]” to find the value of \[\theta \].

Complete step-by-step solution
Here, we have been given a cyclic quadrilateral whose sides are in A.P, so let us draw a diagram of the given situation.

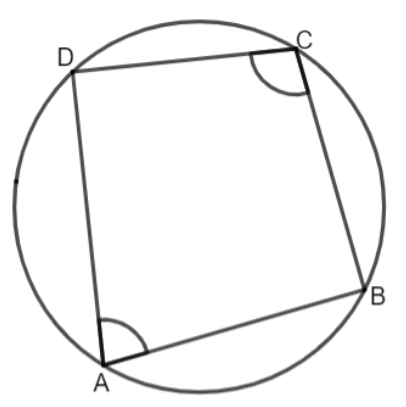
Let us assume the four sides of the quadrilateral as a, a + d, a + 2d, a + 3d starting from the shortest side to the longest side. Here, ‘a’ is the first term of the A.P. and ‘d’ is a common difference.
Now, it is said that the length of the shortest side is 6 and the difference between the length of the longest and the shortest side is also 6. So, we have,
\[\Rightarrow \]Shortest side = a = 6
\[\Rightarrow \] Longest side – shortest side = (a + 3d) – a = 6
\[\Rightarrow \] 3d = 6
\[\Rightarrow \] d = 2
Therefore, substituting the obtained values of ‘a’ and ‘d’ in the expression for the length of all the four sides, we get,
\[\Rightarrow \]a = 6
\[\Rightarrow \] a + d = 6 + 2 = 8
\[\Rightarrow \] a + 2d = 6 + 2 \[\times \] 2 = 10
\[\Rightarrow \] a + 3d = 6 + 2 \[\times \] 3 = 12
Hence, the sides of the quadrilateral are 6, 8, 10, and 12.
Now, we know that the area of a quadrilateral having sides a, b, c and d is given by the formula: -
\[\Rightarrow \] Area = \[\sqrt{\left( s-a \right)\left( s-b \right)\left( s-c \right)\left( s-d \right)-abcd{{\cos }^{2}}\dfrac{\theta }{2}}\]
Here, ‘s’ is the semi – perimeter of the quadrilateral given as: - \[s=\dfrac{a+b+c+d}{2}\] and ‘\[\theta \]’ is the sum of opposite angles of the quadrilateral. Applying the above formula for the given cyclic quadrilateral, we have,
\[\begin{align}
  & \Rightarrow s=\dfrac{6+8+10+12}{2} \\
 & \Rightarrow s=18 \\
\end{align}\]
\[\Rightarrow \] Area = \[\sqrt{\left( 18-6 \right)\left( 18-8 \right)\left( 18-10 \right)\left( 18-12 \right)-6\times 8\times 10\times 12{{\cos }^{2}}\dfrac{\theta }{2}}\]
\[\Rightarrow \] Area = \[\sqrt{12\times 10\times 8\times 6-6\times 8\times 10\times 12{{\cos }^{2}}\dfrac{\theta }{2}}\]
\[\Rightarrow \] Area = \[\sqrt{\left( 6\times 8\times 10\times 12 \right)\left[ 1-{{\cos }^{2}}\left( \dfrac{\theta }{2} \right) \right]}\] - (1)
Now, we know that the sum of opposite angles of a cyclic quadrilateral is \[{{180}^{\circ }}\].
\[\begin{align}
  & \Rightarrow \angle A+\angle C=\angle B+\angle D={{180}^{\circ }} \\
 & \Rightarrow \theta ={{180}^{\circ }} \\
\end{align}\]
Substituting \[\theta ={{180}^{\circ }}\], in equation (1), we get,
\[\Rightarrow \] Area = \[\sqrt{\left( 6\times 8\times 10\times 12 \right)\left[ 1-{{\cos }^{2}}{{90}^{\circ }} \right]}\]
We know that \[\cos {{90}^{\circ }}=0\], so we have,
\[\Rightarrow \] Area = \[\sqrt{\left( 6\times 8\times 10\times 12 \right)\left[ 1-0 \right]}\]
\[\Rightarrow \] Area = \[\sqrt{6\times 8\times 10\times 12}\]
On squaring both sides we get,
\[\Rightarrow \] Area\[^{2}\] = \[6\times 8\times 10\times 12\]
\[\Rightarrow \] Area\[^{2}\] = 5760
Hence, the square of the area of the quadrilateral is 5760.

Note: One may note that we have to consider anyone pair of opposite angles to find the value of \[\theta \]. We can consider either \[\angle A\] and \[\angle C\] or \[\angle B\] and \[\angle D\]. The answer will be the same. Remember that here we have to find the value of the square of the area and not just the area, so you must read the question carefully otherwise you may make a mistake while solving the question in a hurry. You must remember different formulas to find the area of a quadrilateral because anyone can be used according to the situation.