Question

The sides of a triangle are 4, 5 and 6 cm. the area of the triangle is equal to
(a) $\dfrac{15}{4}c{{m}^{2}}$
(b) $\dfrac{15}{4}\sqrt{7}c{{m}^{2}}$
(c) $\dfrac{4}{15}c{{m}^{2}}$
(d) None of these

Answer 1

Hint: Here, we are given that the lengths of the three sides of the triangle are 4, 5 and 6 cm. So, for finding the area of the triangle, we will use Heron’s formula, according to this formula area of a triangle whose sides are of length a, b and c units is give as $Area=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$, here ‘s’ is the semi-perimeter of the triangle given as $s=\dfrac{a+b+c}{2}$.

Complete step-by-step answer:

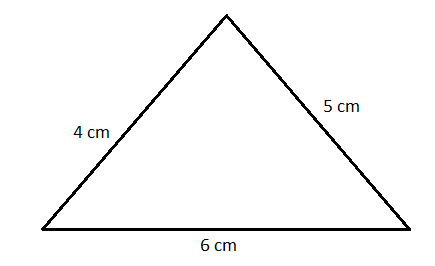
Since, the lengths of the three sides of the triangle are 4 cm, 5 cm and 6 cm. So, the semi-perimeter of this triangle will be:
$s=\dfrac{\left( 4+5+6 \right)cm}{2}=\dfrac{15}{2}cm$
We know that according to Heron’s formula the area of a triangle whose lengths of all three sides are known is given as:
$Area=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}..........\left( 1 \right)$
We have, a = 4 cm, b = 5 cm and c = 6 cm. On substituting all the values in equation (1), we get:
\[\begin{align}
  & Area=\sqrt{\dfrac{15}{2}\left( \dfrac{15}{2}-4 \right)\left( \dfrac{15}{2}-5 \right)\left( \dfrac{15}{2}-6 \right)} \\
 & \Rightarrow Area=\sqrt{\dfrac{15}{2}\times \left( \dfrac{15-8}{2} \right)\times \left( \dfrac{15-10}{2} \right)\times \left( \dfrac{15-12}{2} \right)} \\
 & \Rightarrow Area=\sqrt{\dfrac{15}{2}\times \dfrac{7}{2}\times \dfrac{5}{2}\times \dfrac{3}{2}} \\
 & \Rightarrow Area=\sqrt{\dfrac{15}{2}\times \dfrac{15}{2}\times \dfrac{7}{2}\times \dfrac{1}{2}} \\
 & \Rightarrow Area=\dfrac{15}{2}\sqrt{\dfrac{7}{4}} \\
 & \Rightarrow Area=\dfrac{15}{4}\sqrt{7}c{{m}^{2}} \\
\end{align}\]
So, the area of the triangle is $\dfrac{15}{4}\sqrt{7}c{{m}^{2}}$.
Hence, option (d) is the correct answer.

Note: Students should note that by the word semi-perimeter, we mean half of the perimeter of the triangle. So, for finding the semi-perimeter we just divide the perimeter of the triangle by 2. Calculations which are performed under square root should be carefully done like here we multiplied 5 and 3 which are in the square root to make it 15, so that we can take it out of the square root.