Question

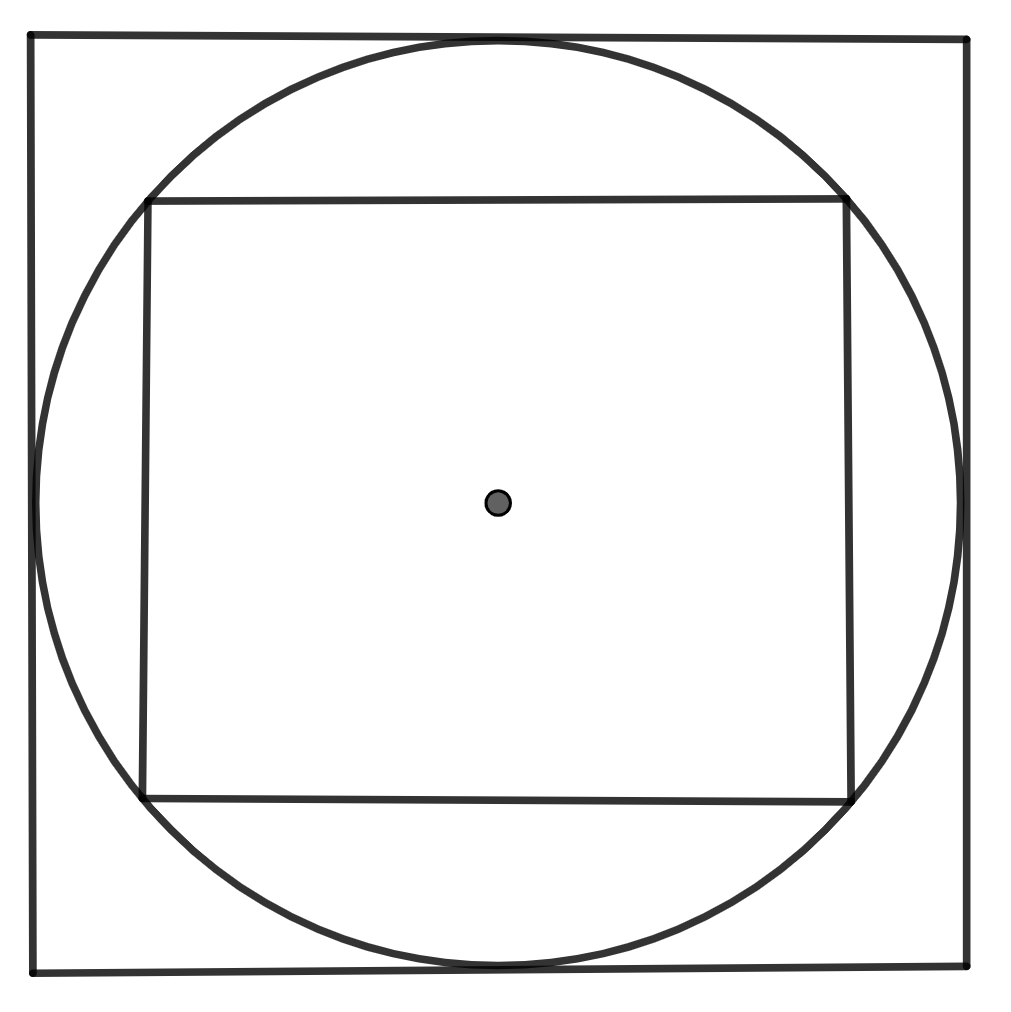
The small square is 100 sq.cm. The area of the large square is sq.cm is

A. 144
B. 165
C. 200
D. 400

Answer 1

Hint: As the area of the square is given, thus, one can find the length of the side by taking the square root of it. Then, find its length of diagonal and by multiplying the side of square with \[\sqrt{2}.\] Then, use the fact that, the diagonal of a square is the length of diameter of the circle which equals the length of the side of the larger square and hence, find its square to find the area of the square.

Complete step-by-step answer:
In the question, we are given a figure in which a circle is given with 2 squares and one is inscribed or considered as a smaller square and the other one is considered as a larger square. We are given that, area of the smaller square is 100 sq.cm. So, from this, we have to find an area of larger squares.
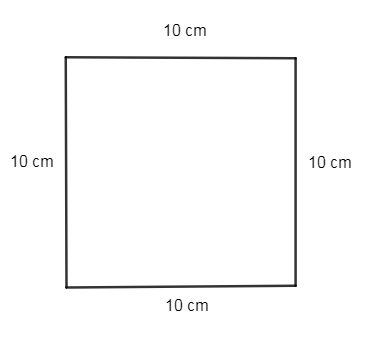
We know that the formula to find the area of a square can be expressed as ${{l}^{2}}$ where l is the length of a square. So, we can say that, ${{l}^{2}}$ equals 100 sq.cm if l is the length of the side of the square. Hence, the value of l is \[\sqrt{100}\Rightarrow 10cm.\]

Then, we will find the diagonal of the square using the formula\[\sqrt{2}l\] , if l is the length of the square. Here, length we found out as 10cm. Hence, the length of diagonal will be \[10\sqrt{2}cm.\]

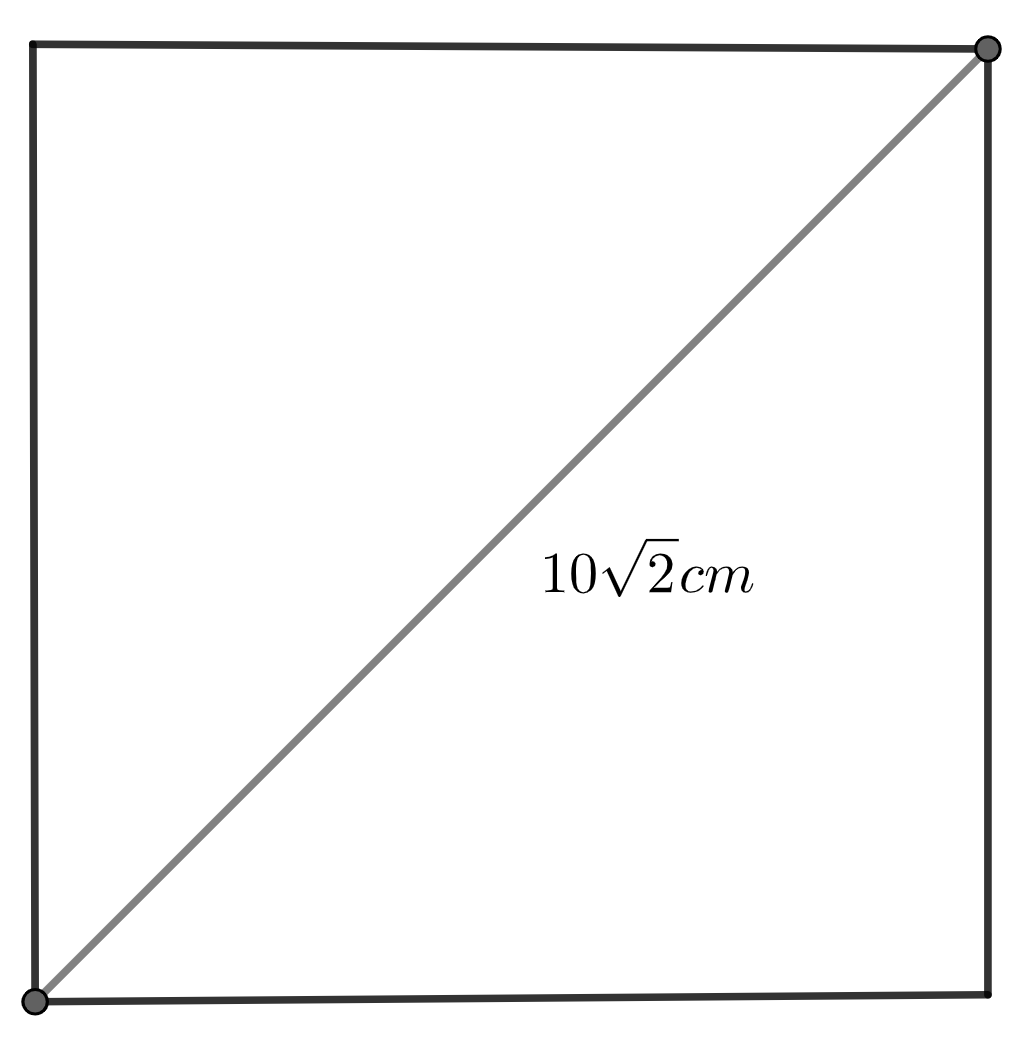
Here, there is a property that, the length of diagonal of inscribed square and the diameter of circle is equal in length. So, from this we can say that, diameter of the circle is \[10\sqrt{2}cm.\]
Now, we will consider the circle and square only, so here, we will use the property that, length of the diameter of the circle equals the length of the side of the square.
So, the length of the side of the square is \[10\sqrt{2}cm.\] Hence, we can find its area using a formula that is, ${{l}^{2}}$where l is the length of the side. Thus, area will be \[{{\left( 10\sqrt{2} \right)}^{2}}\Rightarrow 100\times 2\Rightarrow 200c{{m}^{2}}.\]
Hence, the correct option is C.

Note: Generally in these question, where, similar figure is given of consisting of two squares and circles, we can use the fact that, ratio of length of sides of larger to smaller is \[\sqrt{2}:1.\]Thus, one can use it to find area of either square, if any is given.