Question

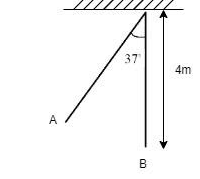
The speed at the final vertical position B of tilt, bob of simple pendulum, when the bob is released from initial position A from rest is $\left( {g = 10m{s^{ - 2}}} \right)$

$
  A.14m/s \\
  B.12m/s \\
  C.4m/s \\
  D.6m/s \\
 $

Answer 1

Hint: The pendulum suspended from a point follows the simple harmonic motion. The simple harmonic motion is defined as a type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position.

Complete step-by-step answer:
Consider the following simple pendulum of length $l$ as shown:

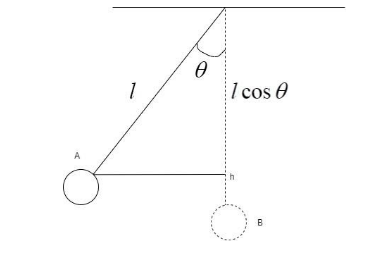
At the extreme position A, the pendulum will have the highest value of potential energy due to its position. When it is released from that position, it is converted to kinetic energy which is maximum at the equilibrium position B.
Potential energy, $P = mgh$
where m=mass of bob, g = acceleration due to gravity and h= height
Kinetic energy, $K = \dfrac{1}{2}m{v^2}$
where v = velocity of the bob.
By conservation of energy, we have –
$
  P = K \\
   \to mgh = \dfrac{1}{2}m{v^2} \\
   \to 2 \times mgh = m{v^2} \\
  \therefore v = \sqrt {2gh} \\
 $
Here, the height should be considered as the distance from the point h in the figure to the position of the bob in B.
To calculate the distance from the geometry,
$
  h = l - l\cos \theta \\
   \to h = l\left( {1 - \cos \theta } \right) \\
 $
Substituting for height in the equation of velocity, we have –
$
  v = \sqrt {2gh} \\
  v = \sqrt {2gl\left( {1 - \cos \theta } \right)} \\
 $
Given,
Acceleration due to gravity,$g = 10m{s^{ - 2}}$
Length,$l = 4m$
Angle of the extreme position, $\theta = {37^ \circ }$
Substituting we get –
$
  v = \sqrt {2gl\left( {1 - \cos \theta } \right)} \\
  v = \sqrt {2 \times 10 \times 4\left( {1 - \cos 37} \right)} \\
$
  Solving,
$
  v = \sqrt {2 \times 10 \times 4\left( {1 - 0.79} \right)} \\
   \to v = \sqrt {2 \times 10 \times 4\left( {0.21} \right)} \\
   \to v = \sqrt {2 \times 10 \times 0.84} \\
   \to v = \sqrt {16.8} \\
   \to v = 4.09m/s \\
 $
Therefore, the velocity at position B, $v = 4m{s^{ - 1}}$

Hence, the correct option is Option C.

Note: In order for a periodic motion to classify as a simple harmonic motion, we have seen that it has to fulfil the basic condition that:
Restoring force, $F \propto - x$ where x is the displacement at every instant.
Now, consider a simple pendulum at its extreme position (or at amplitude):
Note: In order for a periodic motion to classify as a simple harmonic motion, we have seen that it has to fulfil the basic condition that:
Restoring force, $F \propto - x$ where x is the displacement at every instant.
Now, consider a simple pendulum at its extreme position (or at amplitude):

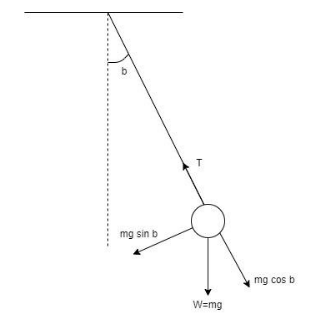
At this position, there are two forces acting on the bob i.e. Tension T and weight W=mg.
Here, the weight can be split into two components namely, $W\cos b$ and $W\sin b$.
The component $mg\sin b$ is responsible for bringing the pendulum back to the mean position and hence, this becomes the restoring force.
Restoring force, $F = - mg\sin b$
Assuming the angle $b$ is very small, $\sin b \simeq b$
Hence,
$F \propto - b$
This means that
$F \propto - x$
Because displacement $x$ is directly proportional to b.
This proves that the oscillation of a simple pendulum is a simple harmonic motion.