Question

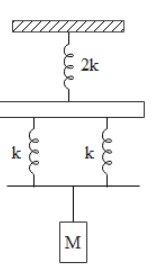
The spring constants of three springs connected to a mass M are as shown in the figure. When mass oscillates, what are the effective spring constants and the time period of vibration?

$
  {\text{A}}{\text{. 4}}k,{\text{ 2}}\pi \sqrt {\dfrac{M}{{4k}}} \\
  {\text{B}}{\text{. 3}}k,{\text{ 2}}\pi \sqrt {\dfrac{M}{3}} k \\
  {\text{C}}{\text{. 2}}k,{\text{ 2}}\pi \sqrt {\dfrac{M}{{2k}}} \\
  {\text{D}}{\text{. none of these}} \\
 $

Answer 1

Hint: When springs are connected in parallel then the resultant spring constant is equal to sum of the individual spring constants while in series combination, the net spring constant gets averaged out. The expression for the time period of a spring system can give the answer for this question.

Formula used:
Combinations of springs: If we have two springs of spring constants ${k_1}$ and ${k_2}$ respectively, then in series combination their resultant spring constant is given as
$\dfrac{1}{k} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}}$
In parallel combination, the resultant spring constant is given as
$k = {k_1} + {k_2}$
The time period of oscillations for a spring mass system is given as
$T = 2\pi \sqrt {\dfrac{m}{k}} $

Complete answer:
We are given a spring mass system, with one spring connected in series with a parallel combination of two other springs, their spring constant as shown in the figure. A mass M is suspended from the bottom of the system which makes the system oscillate due to force exerted by the weight of the mass on the system.
The resultant spring constant of two springs connected in parallel to each other is $k + k = 2k$. They are connected in series with upper spring and their resultant is given as
$
  \dfrac{1}{{k'}} = \dfrac{1}{{2k}} + \dfrac{1}{{2k}} = \dfrac{2}{{2k}} \\
  k' = k \\
 $
This is the value of the resultant spring constant of the springs in the system.
Next we know that the time period of oscillations of the spring mass system is given by the following equation.
$T = 2\pi \sqrt {\dfrac{m}{{k'}}} $
Inserting the value of the resultant spring constant, we get that
$T = 2\pi \sqrt {\dfrac{m}{k}} $

Based on the observed values, we can say that the correct answer is option D as none of the other options are correct.

Note:
The spring mass system executes simple harmonic motion. The various springs have different spring constants but as a whole they exhibit properties of a spring with spring constant k only. Another similar system with a single spring of spring constant k will behave the same as this system.