Question

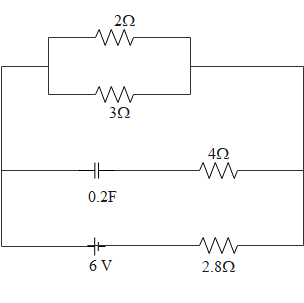
The steady state current in the $2\Omega $ resistor shown in the circuit below is,

$\begin{align}
  & A.0.9A \\
 & B.1.8A \\
 & C.0.45A \\
 & D.0 \\
\end{align}$

Answer 1

Hint: A capacitor can pass electric current through a circuit which is having an ac source as the voltage source. Capacitors will not pass the electricity in dc voltage source. The parallel connected resistors will have the same voltage but different currents. The total current through the battery can be found by dividing the potential supplied with the equivalent resistances. These all may help you to solve this question.

Complete step by step answer:
In the figure we can see that the $2\Omega $ and the $3\Omega $ resistors are connected parallel. So the voltage across the whole branch will be the same. The equivalent resistance through the branch can be written as,
${{\left( {{R}_{eq}} \right)}_{AB}}=\dfrac{2\times 3}{2+3}=1.2\Omega $
This will be the equivalent resistance in the branch AB. As the branch CD is containing a capacitor, and a DC voltage source has been used, the current passing through this branch will be zero. Therefore we can avoid this branch while calculating the current through it.
The total current in the circuit can be found now. As the equivalent resistance in the branch AB is in series with the $2.8\Omega $, the current through each of the branches will be the same. Only the voltage will be different in each branch. Therefore we can write that the total current will be given as,
$I=\dfrac{6}{1.2+2.8}=1.5A$
This will be the total amount of current reaching the AB branch. From there this current will get divided into each resistor as the connection is parallel there. Therefore the current in the $2\Omega $ resistor will be,
${{I}_{1}}=\dfrac{3}{5}\times 1.5=0.9A$
Therefore the current through the $2\Omega $ resistance will be $0.9A$.

So, the correct answer is “Option A”.

Note: When two lights are connected in a parallel circuit each will be having the full voltage of the battery. Therefore the lights in the parallel circuit will be brighter than those in the series circuit. In the parallel circuit, even if one loop is disconnected, then the other loop will remain powered.