Question

The sum of all exterior angles of a triangle is
A.\[{{360}^{0}}\]
B.\[{{180}^{0}}\]
C.\[{{540}^{0}}\]
D.None of these

Answer 1

Hint: Assume a \[\Delta ABC\] in which \[\angle A=\alpha \] , \[\angle B=\beta \] , and \[\angle C=\gamma \] . We know the property that the measure of an exterior angle of a triangle is equal to the sum of the opposite interior angles. Now, using the property we can say that the exterior angle \[\angle ACP\] is equal to the summation of the angles \[\alpha \] and \[\beta \] , \[\angle BAQ\] is equal to the summation of the angles \[\gamma \] and \[\beta \] , and \[\angle CBR\] is equal to the summation of the angles \[\alpha \] and \[\gamma \] .

Complete step-by-step answer:

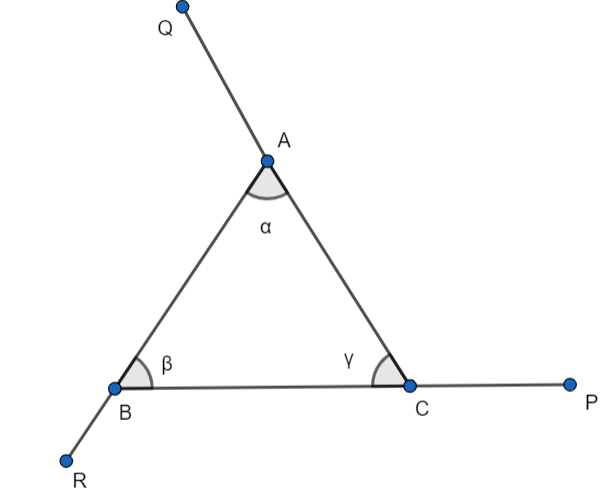
Assume a \[\Delta ABC\] in which \[\angle A=\alpha \] , \[\angle B=\beta \] , and \[\angle C=\gamma \] .
For the angles \[\alpha \] and \[\beta \] , \[\angle ACP\] is an exterior angle.
We know the property that the measure of an exterior angle of a triangle is equal to the sum of the opposite interior angles.
Now, using the property we can say that the exterior angle \[\angle ACP\] is equal to the summation of the angles \[\alpha \] and \[\beta \] .
\[\angle ACP=~\alpha +\beta \] …………………(1)
For the angles \[\gamma \] and \[\beta \] , \[\angle BAQ\] is an exterior angle.
We know the property that the measure of an exterior angle of a triangle is equal to the sum of the opposite interior angles.
Now, using the property we can say that the exterior angle \[\angle BAQ\] is equal to the summation of the angles \[\gamma \] and \[\beta \] .
\[\angle BAQ=~\gamma +\beta \] …………………(2)
For the angles \[\alpha \] and \[\gamma \] , \[\angle CBR\] is an exterior angle.
We know the property that the measure of an exterior angle of a triangle is equal to the sum of the opposite interior angles.
Now, using the property we can say that the exterior angle \[\angle CBR\] is equal to the summation of the angles \[\alpha \] and \[\gamma \] .
\[\angle CBR=~\alpha +\gamma \] …………………(3)
For the \[\Delta ABC\] exterior angles are \[\angle CBR\] , \[\angle BAQ\] , and \[\angle ACP\] .
Now, the sum of all exterior angles,
\[~\angle ACP+\angle BAQ+\angle CBR\] ………………………(4)
From equation (1), equation (2), equation (3), and equation (4), we get
\[\begin{align}
  & ~\angle ACP+\angle BAQ+\angle CBR \\
 & =~\alpha +\beta +~\gamma +\beta +~\alpha +\gamma \\
\end{align}\]
\[=2(\alpha +\beta +\gamma )\] ………………(5)
We know that the sum of all interior angles of a triangle is \[{{180}^{0}}\] .
That is,
\[(\alpha +\beta +\gamma )={{180}^{0}}\] …………………..(6)
From equation (5) and equation (6), we get
\[\begin{align}
  & =2(\alpha +\beta +\gamma ) \\
 & =2\times {{180}^{0}} \\
 & ={{360}^{0}} \\
\end{align}\]
So, the sum of all exterior angles of a triangle is \[{{360}^{0}}\] .
Hence, the correct option is A.

Note: We can also solve this question by using linear pair angles.

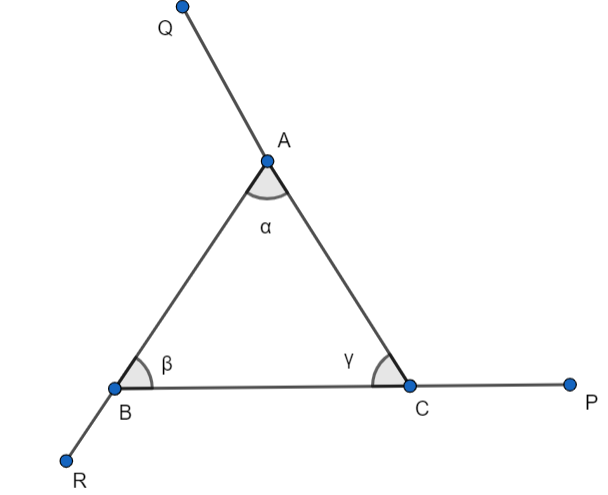
Assume a \[\Delta ABC\] in which \[\angle A=\alpha \] , \[\angle B=\beta \] , and \[\angle C=\gamma \] .
Here, \[\angle ACB\] and \[\angle ACP\] are linear pair angles.
So, \[\angle ACB+\angle ACP={{180}^{0}}\]
\[\angle ACP=~{{180}^{0}}-\gamma \] ……………(1)
Here, \[\angle BAQ\] and \[\angle BAC\] are also linear pair angles.
So, \[\angle BAQ+\angle BAC={{180}^{0}}\]
\[\angle BAQ=~{{180}^{0}}-\alpha \] ……………(2)
Here, \[\angle CBR\]and \[\angle CBA\] are linear pair angles.
So, \[\angle CBR+\angle CBA={{180}^{0}}\]
\[\angle CBR=~{{180}^{0}}-\beta \] ……………(3)
From equation (1), equation (2), and equation (3),
\[\begin{align}
  & ~\angle ACP+\angle BAQ+\angle CBR \\
 & =~~{{180}^{0}}-\gamma +{{180}^{0}}-\alpha +{{180}^{0}}-\beta \\
\end{align}\]
\[={{540}^{0}}-(\alpha +\beta +\gamma )\] ………………….(4)
We know that the sum of all interior angles of a triangle is \[{{180}^{0}}\] .
That is,
\[(\alpha +\beta +\gamma )={{180}^{0}}\] ………………….(5)
From equation (4) and equation (5),
\[\begin{align}
  & ={{540}^{0}}-(\alpha +\beta +\gamma ) \\
 & ={{540}^{0}}-{{180}^{0}} \\
 & ={{360}^{0}} \\
\end{align}\]
So, the sum of all exterior angles of a triangle is \[{{360}^{0}}\] .