Answer
Verified400.2k+ views
Hint: The sum of the angles a concave quadrilateral can be found by dividing the quadrilateral into two triangles and using the angle sum property of a triangle that sum of all the angles of a triangles is always $180{}^\circ $.
Complete step-by-step answer:
We have to find the sum of angles of a concave quadrilateral.
Concave quadrilaterals are four sided polygons that have one interior angle greater than $180{}^\circ $.
We can identify concave quadrilaterals by using the fact that one of its diagonals lie partially or completely outside the quadrilateral.
Consider the below concave quadrilateral ABCD:
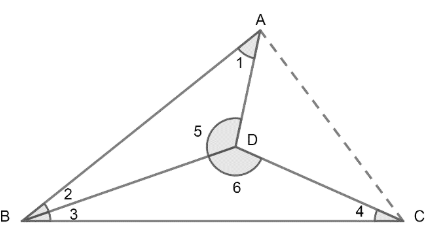
We can see that its one interior angle $\angle ADC$ is greater than $180{}^\circ $ and also its one diagonal AC lies completely outside the quadrilateral.
Thus, it is a concave quadrilateral we have to find the sum of its all the interior angles.
Let’s divide this concave quadrilateral into two triangles by drawing a line BD,
Now, two triangles are formed: $\Delta ABD\ and\ \Delta BDC$,
By angle sum property of a triangle, the sum of all the angles of a triangle is always $180{}^\circ $.
Using this property, we can write,
Sum of all the angles of $\Delta ABD=180{}^\circ $
$\Rightarrow \angle 1+\angle 2+\angle 5=180{}^\circ .........\left( 1 \right)$
And sum of all the angles of $\Delta BDC=180{}^\circ $
$\Rightarrow \angle 3+\angle 6+\angle 4=180{}^\circ .........\left( 2 \right)$
Adding equation (1) and (2), we will get,
$\begin{align}
& \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6=180{}^\circ +180{}^\circ \\
& \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6=360{}^\circ .................\left( 3 \right) \\
\end{align}$
From the diagram of concave quadrilateral above, we can observe that,
$\begin{align}
& \angle A\ of\ quadrilateral\ =\angle 1 \\
& \angle B\ of\ quadrilateral\ =\angle 2+\angle 3 \\
& \angle C\ of\ quadrilateral\ =\angle 4 \\
& \angle D\ of\ quadrilateral\ =\angle 5+\angle 6 \\
\end{align}$
Using the above relations,
On replacing $\angle 1\ with\ \angle A,\ \left( \angle 2+\angle 3 \right)\ with\ \angle B,\ \angle 4\ with\ \angle C\ and\ \left( \angle 5+\angle 6 \right)\ with\ \angle D$in equation (3), we will get,
$\Rightarrow \angle A+\angle B+\angle C+\angle D=360{}^\circ $
Hence the required sum of all the angles of a concave quadrilateral is $360{}^\circ $.
Note: As with any simple polygon, the sum of the interior angles of a concave polynomial is $180{}^\circ \times \left( n-2 \right)$ where $'n'$is the number of sides.
It is always possible to partition a concave polynomial into a set of convex polynomials.
Complete step-by-step answer:
We have to find the sum of angles of a concave quadrilateral.
Concave quadrilaterals are four sided polygons that have one interior angle greater than $180{}^\circ $.
We can identify concave quadrilaterals by using the fact that one of its diagonals lie partially or completely outside the quadrilateral.
Consider the below concave quadrilateral ABCD:
We can see that its one interior angle $\angle ADC$ is greater than $180{}^\circ $ and also its one diagonal AC lies completely outside the quadrilateral.
Thus, it is a concave quadrilateral we have to find the sum of its all the interior angles.
Let’s divide this concave quadrilateral into two triangles by drawing a line BD,
Now, two triangles are formed: $\Delta ABD\ and\ \Delta BDC$,
By angle sum property of a triangle, the sum of all the angles of a triangle is always $180{}^\circ $.
Using this property, we can write,
Sum of all the angles of $\Delta ABD=180{}^\circ $
$\Rightarrow \angle 1+\angle 2+\angle 5=180{}^\circ .........\left( 1 \right)$
And sum of all the angles of $\Delta BDC=180{}^\circ $
$\Rightarrow \angle 3+\angle 6+\angle 4=180{}^\circ .........\left( 2 \right)$
Adding equation (1) and (2), we will get,
$\begin{align}
& \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6=180{}^\circ +180{}^\circ \\
& \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6=360{}^\circ .................\left( 3 \right) \\
\end{align}$
From the diagram of concave quadrilateral above, we can observe that,
$\begin{align}
& \angle A\ of\ quadrilateral\ =\angle 1 \\
& \angle B\ of\ quadrilateral\ =\angle 2+\angle 3 \\
& \angle C\ of\ quadrilateral\ =\angle 4 \\
& \angle D\ of\ quadrilateral\ =\angle 5+\angle 6 \\
\end{align}$
Using the above relations,
On replacing $\angle 1\ with\ \angle A,\ \left( \angle 2+\angle 3 \right)\ with\ \angle B,\ \angle 4\ with\ \angle C\ and\ \left( \angle 5+\angle 6 \right)\ with\ \angle D$in equation (3), we will get,
$\Rightarrow \angle A+\angle B+\angle C+\angle D=360{}^\circ $
Hence the required sum of all the angles of a concave quadrilateral is $360{}^\circ $.
Note: As with any simple polygon, the sum of the interior angles of a concave polynomial is $180{}^\circ \times \left( n-2 \right)$ where $'n'$is the number of sides.
It is always possible to partition a concave polynomial into a set of convex polynomials.