Question

The sum of the focal distances from any point on the ellipse \[9{x^2} + 16{y^2} = 144\] is
1. \[3\]
2. \[6\]
3. \[8\]
4. \[4\]

Answer 1

Hint: We are given the equation of an ellipse and we are asked to find the sum of the focal distances from any point on the given ellipse. Firstly we need to keep in mind the definition of an ellipse. An ellipse is a curve consisting of two focal points, such that all the points lying on the curve have the sum of the two distances from the focal points as constant. We have to find this constant distance of each point of the ellipse from the two foci.

Complete step-by-step solution:

We are given the equation of ellipse as \[9{x^2} + 16{y^2} = 144\]
Converting it to the standard form of the equation of ellipse we get ,
\[\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1\]
Comparing it with the general equation of ellipse i.e. \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] we get \[a = 4\] and \[b = 3\]
Now, we know that the sum of focal distances of a point on an ellipse is constant and equal to the length of the major axis of that particular ellipse i.e. sum of focal distance of any point on an ellipse \[ = 2a\]
So. substituting the known value of a, we get,
\[ = 2 \times 4 = 8\]
Therefore option (3) is the correct answer.

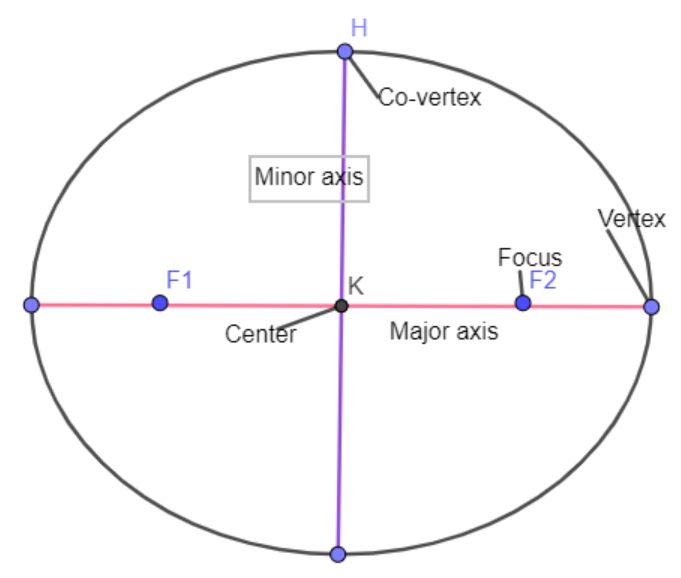
Note: In order to solve such types of questions one must have a grip over the concept of ellipses , related terms and the respective formulas. Major axis is denoted by a and is the greatest length of any ellipse passing through the center from one end to the other, at the broad part of the ellipse. On the other hand, the minor axis is denoted by b and is the shortest diameter of the ellipse, crossing through the center at the narrowest part. Half of the major axis is called semi-major axis and half of the minor axis is called semi-minor axis.