Question

The thermo emf $E$(in volts) of a certain thermocouple is found to vary with $Q$(in$C$) according to the equation ($E=20Q-\dfrac{{{Q}^{2}}}{20}$, where $Q$is temperature and of the hot function, the cold function being kept at${{0}^{\circ }}C$. Then, the neutral temperature of the thermocouple is
$\text{A}\text{. 30}{{0}^{\circ }}C$
$\text{B}\text{. 40}{{0}^{\circ }}C$
$\text{C}\text{. 10}{{0}^{\circ }}C$
$\text{D}\text{. 20}{{0}^{\circ }}C$

Answer 1

Hint: When two metals are placed at different temperatures, the temperature of the junctions remains different and it results in the development of an electric field across the two junction circuits. In case of a thermocouple made from similar materials, voltage across both wires or junctions would be the same. Differentiating it with respect to temperature would give a zero value.

Formula used:
For thermocouple made of similar metal, $\dfrac{dE}{dQ}=0$

Complete step-by-step solution -
Thermo emf is an electromotive force which is generated due to thermal gradient. The emf set up in a thermocouple, when its two junctions are kept at different temperatures is called a thermo emf. It is developed while keeping one junction at${{0}^{\circ }}C$. Value of thermo emf depends upon the nature of metals and temperature of junctions.
When two dissimilar metals are in contact, some free electrons diffuse from one metal (having lower work function) to the other metal (having higher work function). Thus one metal becomes positively charged and the other becomes negatively charged. This process continues until the difference developed is known as contact emf.

The direction and magnitude of contact emf depend upon what metals are used and the temperature of the junction. When copper is brought in contact with iron, more free electrons diffuse from iron to copper, thus making iron positive with respect to copper as.

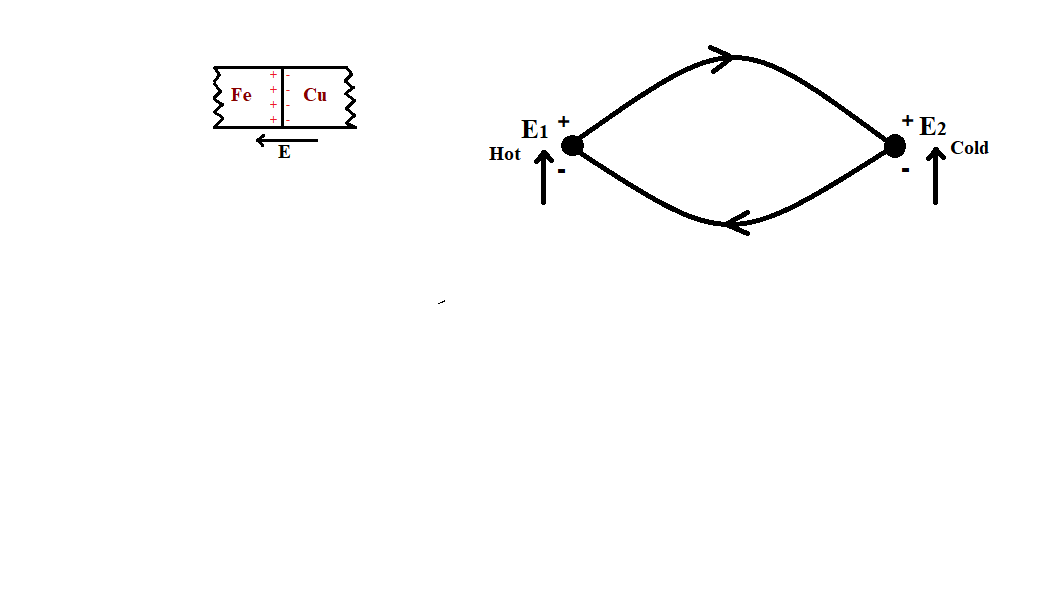
When the junction of the metals forming the thermocouple are at the same temperature .the two contact electromotive forces, ${{E}_{1}}$and ${{E}_{2}}$, are equal in magnitude and of opposite polarity. However, if the two junctions of the thermocouple are at different temperatures, the contact emf at the hot junction is more than at the cold junction.

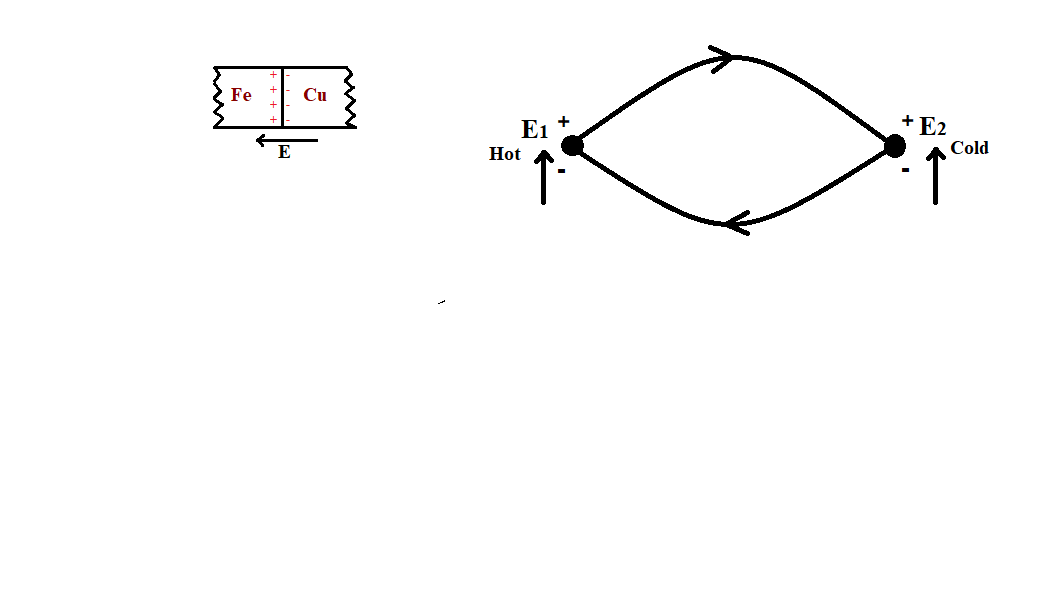
When a thermocouple made from two similar metals is heated to create a temperature gradient, the voltage across each wire would be the same. These voltages cancel out each other and result would be zero voltage across the two wires at all temperatures.
We are given,
 $E=20Q-\dfrac{{{Q}^{2}}}{20}$
Differentiating with respect to$Q$
$\dfrac{dE}{dQ}=\dfrac{d\left( 20Q-\dfrac{{{Q}^{2}}}{20} \right)}{dQ}$
For thermocouple made of similar metal, we have,
$\dfrac{dE}{dQ}=0$
 \[\begin{align}
  & \dfrac{d\left( 20Q-\dfrac{{{Q}^{2}}}{20} \right)}{dQ}=0 \\
 & 20-\dfrac{2Q}{20}=0 \\
 & 400-2Q=0 \\
 & Q=\dfrac{400}{2}=200 \\
\end{align}\]
$Q={{200}^{\circ }}C$
The neutral temperature of the thermocouple is ${{200}^{\circ }}C$
Hence, the correct option is D.

Note:When two metals are kept at different temperatures, it generates different junction temperatures for two metals. Thus, there is a net emf in the thermocouple and thermoelectric current flow in a particular direction. It may be noted that contact emf depends only on the work function of the metals, not on the size of metal or area of contact between metals.