Question

The thermo emf of a hypothetical thermocouple varies with the temperature Ѳ of the hot junction as $E=a\theta +b{{\theta }^{2}}$ in volts, where the ratio $\dfrac{a}{b}\text{ is }{{700}^{\circ }}C.$ If the cold junction is kept at ${{0}^{\circ }}C$, then the neutral temperature is :
\[\begin{array}{*{35}{l}}
   \text{a) 70}{{\text{0}}^{\text{o}}}\text{C} \\
   \text{b) 140}{{\text{0}}^{\text{o}}}\text{C} \\
   \text{c) 39}{{\text{0}}^{\text{o}}}\text{C} \\
\end{array}\]
d) No neutral temperature is possible for this thermocouple

Answer 1

Hint: The above equation for emf of a thermocouple represents an inverted parabola on the y axis if we consider the emf to be on y-axis and the temperature to be on x-axis. The neutral temperature of a thermocouple is the temperature at which the emf of the thermocouple is maximum. For any curve in general if the quantity Y on the y-axis varies with a quantity X on the x-axis then we say that the maximum value of Y is given as $\dfrac{dY}{dX}=0$. Using this condition we can find the neutral temperature.

Complete step by step answer:
Let us first see how the emf of a thermocouple varies with temperature.

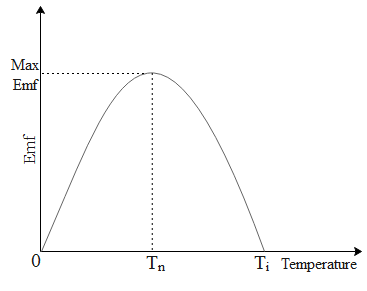
A thermocouple consists of two dissimilar metals connected together to form a closed circuit. One of the junctions is kept at high temperature and the other junction is usually kept at ${{0}^{\circ }}C$. This difference in temperatures at two different junctions generates an emf called as the thermo emf.
This thermo emf is maximum at a temperature called as neutral temperature ${{\text{T}}_{\text{n}}}$. If we further keep on increasing the temperature the emf generated keeps on decreasing and reaches to zero at a temperature called as the inversion temperature${{\text{T}}_{\text{i}}}$.
Let us now use the condition for maximum emf i.e. $\dfrac{dE}{d\theta }=0$ This condition comes from the fact that the slope of the above curve to its maximum value is zero.
Hence differentiating the equation of thermo emf with respect to temperature we get
$\dfrac{dE}{d\theta }=a\dfrac{d\theta }{d\theta }+b\dfrac{d{{\theta }^{2}}}{d\theta }$
$\dfrac{dE}{d\theta }=a+2b\theta $
Since $\dfrac{dE}{d\theta }=0$and further differentiating the above equation we get,
$0=a+b2\theta$
Further this can be written as,
$\theta =-\dfrac{\text{a}}{\text{2b}}.....(1)$ here $\text{ }\!\!\theta\!\!\text{ }$ is the value of maximum temperature. It is given in the question that $\dfrac{a}{b}\text{ is }{{700}^{\circ }}C.$ Substituting this in equation 1 we get,
$\text{ }\!\!\theta\!\!\text{ =-}\dfrac{700}{\text{2}}=-{{350}^{\circ }}C$
The neutral temperature of the thermocouple cannot be negative since the cold junction itself is at 0 degree Celsius.

Hence the correct answer is option d.

Note:
If we keep on increasing the temperature even after the thermocouple reaches an inversion temperature the emf will be generated, but it will now be in the opposite direction. Initially if the current was flowing from cold to hot junction, as soon as the temperature crosses the inversion temperature current will flow from hot to cold junction. One more thing we can also generalize is that, if the value of a by b for a thermocouple is positive it cannot have an inversion temperature.