Question

The thickness of a hollow cylinder is 2cm. It is 35 cm long and its inner radius is 12 cm. Find the volume of metal required to make the cylinder, assuming it is open, at either end.

Answer 1

Hint: We have the inner radius of the cylinder and its thickness is 12 cm and 2 cm respectively. Using the inner radius and thickness get the outer radius of the cylinder. We know that the volume of the cylinder is \[\pi {{r}^{2}}h\] . Now, using inner radius and outer radius calculate the volume of the inner cylinder and outer cylinder. The volume of the required metal = Volume of the outer cylinder - Volume of the inner cylinder. Use this and solve it further.

Complete step-by-step answer:
According to the question, it is given that the inner radius, height, and thickness of the cylinder are 12 cm, 35 cm, and 2 cm respectively.
We have to find the volume required to make the cylinder, assuming it is open, at either end.

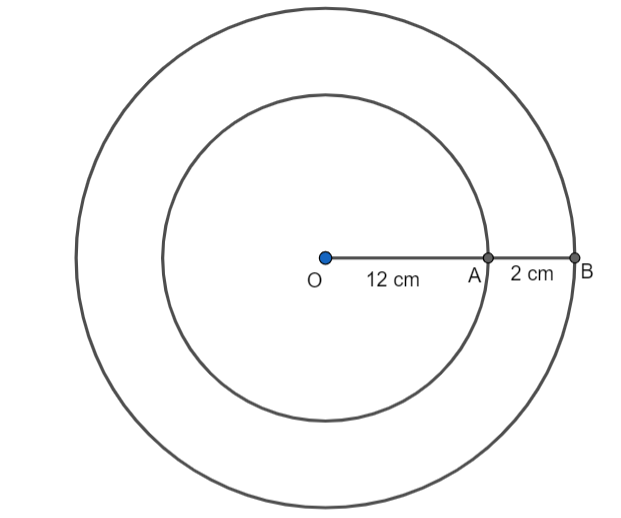
Here, OA is the inner radius.
The radius of the inner circle is OA = 12 cm.
The thickness of the hollow cylinder is the distance AB.
The radius of the outer circle OB= OA+AB= \[12+2=14\] cm.
The height of the cylinder = 35 cm.
We know that the volume of the cylinder is \[\pi {{r}^{2}}h\] .
Volume of outer cylinder = \[\pi {{r}^{2}}h=\dfrac{22}{7}\times 14\times 14\times 35\,c{{m}^{3}}=22\times 28\times 35\,c{{m}^{3}}\] = 21,560 \[c{{m}^{3}}\] .
The volume of the inner cylinder = \[\pi {{r}^{2}}h=\dfrac{22}{7}\times 12\times 12\times 35\,c{{m}^{3}}=\dfrac{110880}{7}c{{m}^{3}}\] .
We have to find the volume of the metal required to make the hollow cylinder.
For the volume of the hollow cylinder, we have to remove the volume of the inner cylinder from the outer cylinder.
The volume of the required metal = Volume of the outer cylinder - Volume of the inner cylinder
\[\begin{align}
  & 21560-\dfrac{110880}{7}c{{m}^{3}} \\
 & =\dfrac{150920-110880}{7}c{{m}^{3}} \\
 & =\dfrac{40040}{7}c{{m}^{3}} \\
 & =5720c{{m}^{3}} \\
\end{align}\]
Hence, the volume of metal required to make the hollow cylinder is \[5720c{{m}^{3}}\] .

Note: In this question, one might find the volume of the inner cylinder and conclude it as the volume of the hollow cylinder which is wrong. The volume of the hollow cylinder is not the same as the volume of the inner cylinder. Therefore, to get the volume of the hollow cylinder, we have to deduct the volume of the inner cylinder from the volume of the outer cylinder.
We can also solve this question using direct formula,
Volume of hollow cylinder = \[\pi \left( {{r}_{1}}^{2}-{{r}_{2}}^{2} \right)h\] .
where, \[{{r}_{1}}\] is the outer radius,
\[{{r}_{2}}\] is the inner radius, and h is the height of the cylinder.
Here, the outer radius is 14cm, inner radius is 12cm and height is 35 cm.
Volume of hollow cylinder = \[\pi \left( {{r}_{1}}^{2}-{{r}_{2}}^{2} \right)h=\dfrac{22}{7}\left( {{14}^{2}}-{{12}^{2}} \right)35=22(196-144)5=110\times 52=5720c{{m}^{3}}\] .
Hence, the volume of metal required to make the hollow cylinder is \[5720c{{m}^{3}}\] .