
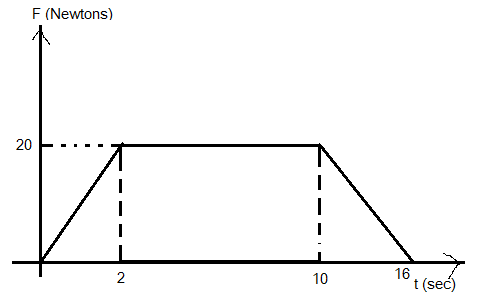
The thrust (F) versus time graph of a rocket is shown in the figure. The mass of the rocket is 1200g. Then the velocity of the rocket after 16 seconds starting from rest (Neglect the gravity)
A.
B.
C.
D.

Answer
485.4k+ views
Hint: In the given question, change the force-time curve into the acceleration-time curve since acceleration is the change in velocity of time by using newton’s second law of motion. Newton’s second law of motion states the acceleration of an object produced by a net force is proportional to the mass of that object. For the result, we need to find the area under the acceleration-time curve.
Complete step by step answer:
Given the mass of the rocket is 1200 grams and from the figure, it can be observed that the maximum force is 20 newton. From the newton’s second law of motion, we can write,
Substitute 1200 grams (or 1200/1000 kilograms) for mass and 20 newtons for the force in the formula
Now we can draw acceleration time graph as
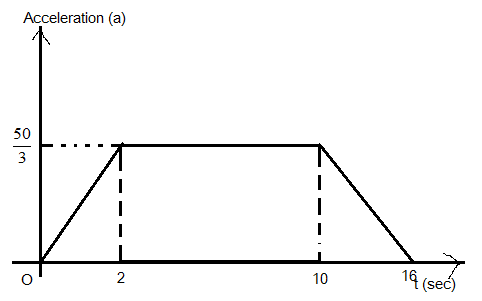
Now the area in the acceleration-time graph changes with velocity hence we can say
Change in velocity= area under the graph which equals to the area of the rectangle and two areas of the triangles.
Since the objects start from rest so we can say
Hence the velocity of the rocket will be
Therefore the velocity of the rocket after 16 seconds starting from rest is
So, the correct answer is “Option D”.
Note:
As we know the area under a curve is the same as the definite integral between two fixed points hence we can also use the method of integration to find the change in momentum. Moreover, the given curve is between thrust (force) and the time but we need the velocity which can be determined by the acceleration-time curve, so it should be transformed accordingly.
Complete step by step answer:
Given the mass of the rocket is 1200 grams and from the figure, it can be observed that the maximum force is 20 newton. From the newton’s second law of motion, we can write,
Substitute 1200 grams (or 1200/1000 kilograms) for mass and 20 newtons for the force in the formula
Now we can draw acceleration time graph as

Now the area in the acceleration-time graph changes with velocity hence we can say
Change in velocity= area under the graph which equals to the area of the rectangle and two areas of the triangles.
Since the objects start from rest so we can say
Hence the velocity of the rocket will be
Therefore the velocity of the rocket after 16 seconds starting from rest is
So, the correct answer is “Option D”.
Note:
As we know the area under a curve is the same as the definite integral between two fixed points hence we can also use the method of integration to find the change in momentum. Moreover, the given curve is between thrust (force) and the time but we need the velocity which can be determined by the acceleration-time curve, so it should be transformed accordingly.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write a short note on Franklands reaction class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE




