Question

The time taken by the bob of a pendulum to complete one oscillation is called its:
A. amplitude
B. time period
C. frequency
D. oscillation

Answer 1

Hint: The pendulum suspended from a point follows the simple harmonic motion. The simple harmonic motion is defined as a type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position.

Complete step-by-step answer:
The simple harmonic motion of the pendulum causes about a type of motion known as oscillation. Oscillation is defined as a repetitive variation with time of a particular value viz. displacement, velocity etc. between two or more states.
These oscillations can be represented on a graph as shown:

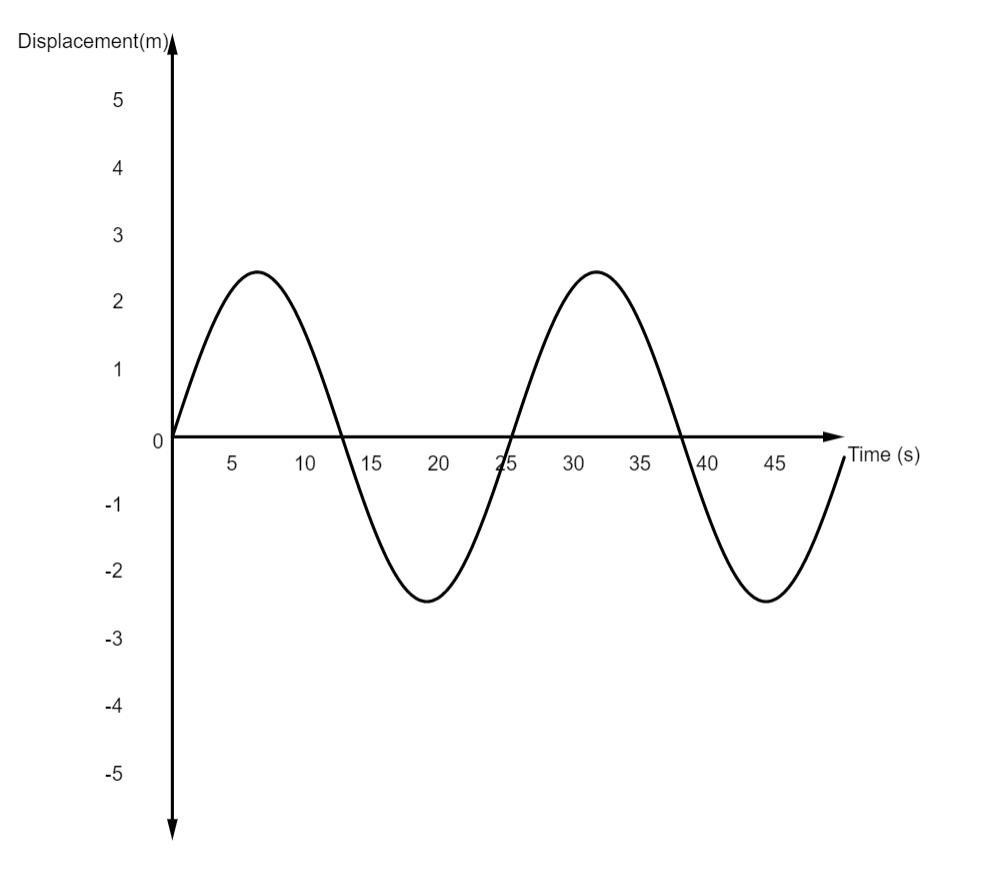
Here, one oscillation is represented by one complete wave. There are different properties associated with a wave. They are:
a. Amplitude: It is the maximum displacement occurring in one cycle of the wave. It is measured in the units of displacement such as cm or m. b. Frequency: It is equal to the number of wave cycles occurring in one second. It is measured in a unit called hertz (Hz). c. Time period: It is the time taken by the body to complete one oscillation cycle. It is measured in seconds (sec).

As per the question, the time taken by the pendulum to complete one oscillation is called the time period.

Hence, the correct option is Option B.

Note: In order for a periodic motion to classify as a simple harmonic motion, we have seen that it has to fulfil the basic condition that:
Restoring force, $F \propto - x$ where x is the displacement at every instant.
Now, consider a simple pendulum at its extreme position (or at amplitude):

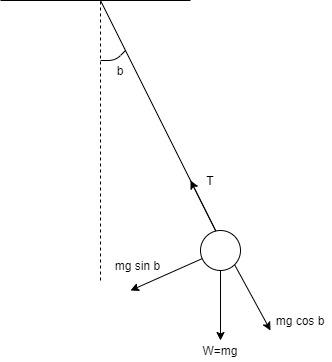
At this position, there are two forces acting on the bob i.e. Tension T and weight W=mg.
Here, the weight can be split into two components namely , $W\cos b$and $W\sin b$.
The component $mg\sin b$is responsible for bringing the pendulum back to the mean position and hence, this becomes the restoring force. Restoring force, $F = - mg\sin b$ Assuming the angle $b$is very small, $\sin b \simeq b$ Hence,
$
  F = - mgb \\
 $
This proves that the oscillation of a simple pendulum is a simple harmonic motion.