Question

The total length of the sonometer wire between fixed ends is 110 cm. Two bridges are placed to divide the length of wire in ratio 6:3:2. The tension in the wire is 400N and the mass per unit length is 0.01 kg per ‘m’. What is the minimum common frequency with which three parts can vibrate?
$A. {\text{ }}1100Hz \\
  B. {\text{ 1000Hz}} \\
  C. {\text{C 166Hz}} \\
  D. {\text{D 100Hz}} \\
 $

Answer 1

Hint- You can start by briefly explaining the sonometer. Then make a diagram for the given situation with the wire divided into three parts. Then calculate the length of wire in each part by using the given ratio of the length of all the three parts, i.e. $6:3:2$ . Then use the equation $f = \dfrac{1}{{2l}}\sqrt {\dfrac{T}{m}} $ to find the frequency of the sound produced by each part and then find a common frequency to reach the solution.

Complete step-by-step solution -
A sonometer is an equipment that we use to calculate the relation between the frequency of the sound produced by plucking a string, the tension in the wire, the length of the string, and the mass per unit length. This relationship is called Mersenne’s law.
Here we know that the total length of the wire is $110cm = 1.1m$
We also know that the length of the three parts are in the ratio $6:3:2$
So, the length of the first part is $0.6m$.
The length of the second part is $0.3m$.
The length of the third part is $0.2m$.

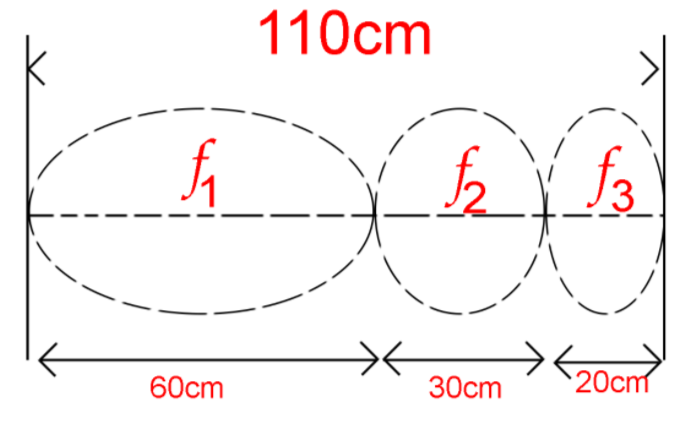
We are also given that the mass per unit length $ = 0.1kg/m$ and the tension in all the three parts is $400N$.
We know, that the frequency of the sound wave produced by plucking the string (or the frequency of the waves formed in the string when they are plucked) is
$f = \dfrac{1}{{2l}}\sqrt {\dfrac{T}{m}} $
Here, $f = $ Frequency
$l = $ Length
$T = $ Tension
$m = $ Mass per unit length
So, for the first part, we have
${f_1} = \dfrac{1}{{2 \times 0.6}}\left( {\sqrt {\dfrac{{400}}{{0.01}}} } \right)$
${f_1} = \dfrac{1}{{2 \times 0.6}}\left( {200} \right) = \dfrac{{1000}}{6}Hz$
For the second part, we have
${f_2} = \dfrac{1}{{2 \times 0.3}}\left( {\sqrt {\dfrac{{400}}{{0.01}}} } \right)$
\[{f_2} = \dfrac{1}{{2 \times 0.3}}\left( {200} \right) = \dfrac{{1000}}{3}Hz\]
For the third part, we have
${f_{ 3}} = \dfrac{1}{{2 \times 0.2}}\left( {\sqrt {\dfrac{{400}}{{0.01}}} } \right) $
$ {f_{ 3}} = \dfrac{1}{{2 \times 0.2}}\left( {200} \right) = \dfrac{{1000}}{2}Hz $
Hence, the common frequency is \[1000Hz\] .
Hence, option B is the correct choice.

Note- When we pluck a string in a sonometer the wire vibrates and produces sound. The plucked wire has vibrations that form a wave that goes to and fro between the ends of the wire. The frequency of the sound wave produced is the same as the frequency of the wave that is produced in the plucked wire.