Question

The total surface area of a frustum of a frustum cone is $450{{m}^{2}}$. The diameter of the top cone is 2 m and the bottom cone is 5 m. What is the curved surface area of the frustum cone?
(a) $410.25{{m}^{2}}$
(b) $428.25{{m}^{2}}$
(c) $420.32{{m}^{2}}$
(d) $430.02{{m}^{2}}$

Answer 1

Hint: First draw the figure of a frustum of a cone according to the given conditions. Assume the radius of the top cone as r and the bottom cone as R, height of the frustum part as h and the slant height as l. Find the values of r and R using the relations $\text{radius=}\dfrac{\text{diameter}}{2}$. Now, use the formula for the total surface area of a frustum given as $T.S.A=\pi \left( r+R \right)l+\pi \left( {{r}^{2}}+{{R}^{2}} \right)$ where $C.S.A=\pi \left( R+r \right)l$, C.S.A denotes the curved surface area. Leave this C.S.A expression as it is and evaluate other terms to get the answer.

Complete step by step solution:
Here we have been provided with a frustum of a cone with provided dimensions and the total surface area (T.S.A). We are asked to find the curved surface area (C.S.A) of this frustum cone. First let us draw the figure of the frustum of provided dimensions.

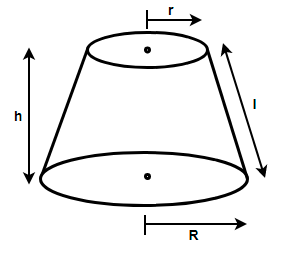
In the above figure we have considered the radius of the top cone as r and that of the bottom cone as R. also we have considered the height of the cone as h and the slant height as l.
Now, we know that the total surface area of a cone is given as $T.S.A=\pi \left( r+R \right)l+\pi \left( {{r}^{2}}+{{R}^{2}} \right)$. This expression also includes the curved surface area part given as $C.S.A=\pi \left( R+r \right)l$, so we can write the above expression as:
$\begin{align}
  & \Rightarrow T.S.A=C.S.A+\pi \left( {{r}^{2}}+{{R}^{2}} \right) \\
 & \Rightarrow C.S.A=T.S.A-\pi \left( {{r}^{2}}+{{R}^{2}} \right)..........\left( i \right) \\
\end{align}$
Since, we have been provided with the diameters of the two cones, so we need to find the radius of these cones. We know that $\text{radius=}\dfrac{\text{diameter}}{2}$, so we get,
$\Rightarrow r=\dfrac{2}{2}=1m$ and $R=\dfrac{5}{2}m$
Substituting the given values $T.S.A=450{{m}^{2}},r=1,R=\dfrac{5}{2}$ and $\pi =3$ in equation (i) we get,
\[\begin{align}
  & \Rightarrow C.S.A=450-3\left( {{1}^{2}}+{{\left( \dfrac{5}{2} \right)}^{2}} \right) \\
 & \Rightarrow C.S.A=450-3\left( 1+\dfrac{25}{4} \right) \\
 & \Rightarrow C.S.A=450-21.75 \\
 & \Rightarrow C.S.A=428.25{{m}^{2}} \\
\end{align}\]

So, the correct answer is “Option B”.

Note: You can also find the curved surface area by using the relation $C.S.A=\pi \left( R+r \right)l$. However, here you will be required to find the slant height first so it will be a bit lengthy process. The relation of slant height if given as $l=\sqrt{{{\left( R-r \right)}^{2}}+{{h}^{2}}}$. Remember the relation between the radius and diameter and do not consider the value of diameter in the formula, it happens sometimes in a hurry so be careful at that part.