
The two coherent sources of equal intensity produce maximum intensity of $100$ units at a point. If the intensity of one source is reduced by $36$% by reducing its width then the intensity of light at the same point will be
a. $90$
b. $89$
c. $67$
d. $81$
Answer
548.1k+ views
Hint: To solve the given problem we need to calculate the intensities of the two sources separately and then we need to add the intensities to get the maximum intensity.
Formula used:
The resultant intensity,
${I_R} = {I_1} + {I_2} + 2\sqrt {{I_1}} \sqrt {{I_2}} \cos \phi $
Where, $\phi = 0$.
To find the maximum intensity,
${I_{\max }} = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} $
Complete step by step answer:
In the question, it is given that the two coherent sources of equal intensity produce maximum intensity of $100$ units.
We can consider the Young’s double slit experiment for better understanding.
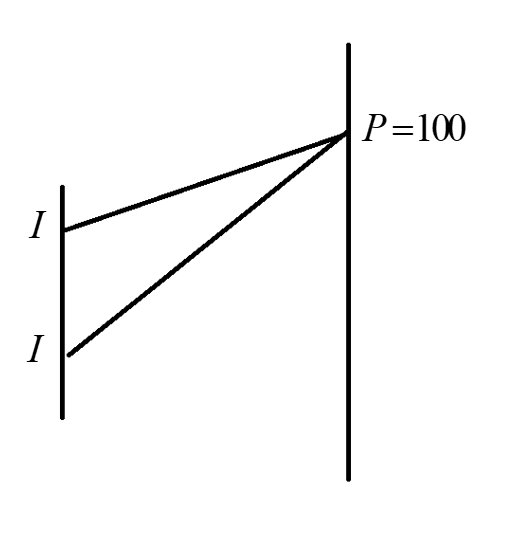
In this diagram, the intensities of the two sources are given and it is represented as $I$and$P$is the maximum intensity of $100\% $. The two sources have equal intensities.
We can consider the maximum intensity. The maximum intensity is given as,
$ {I_{\max }} = {(\sqrt {{I_1}} + \sqrt {{I_2}} )^2}$
We can simplify the given equation as
$ \Rightarrow {I_{\max }} = 2{(\sqrt I )^2}$
$ \Rightarrow 4I$
In the question it is given that maximum intensity $100$ and the intensity of one source is calculated as,
$ \Rightarrow I = \dfrac{{100}}{4}$
$ \Rightarrow I = 25$
We have calculated the intensities of the two coherent sources. The intensity value of one source is $25$. Both the intensities are equal and hence the value of another intensity is also $25$. We can represent these values in the given diagram.
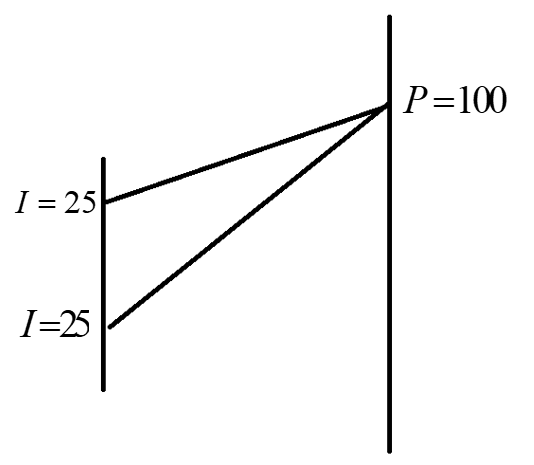
In the question they said that one of the intensities is reduced into $36$% of its width. We can consider the reduced intensity as new intensity that is ${I_{new}}$. Let us consider the ${I_1}$ as ${I_{new}}$.
$ \Rightarrow {I_{new}} = (25 - 25) \times \dfrac{{36}}{{100}}$
$ \Rightarrow 16$ units
Now we have the value of ${I_{new}}$ as $16$ units and ${I_2}$ as $25$. With the help of these values we can calculate the intensity of the light at the same point.
From the resultant intensity we can derive the formula for the maximum intensity. That is,
$ {I_R} = {I_1} + {I_2} + 2\sqrt {{I_1}} \sqrt {{I_2}} \cos \phi $
The value of $\cos \phi $ is $0$.
$ \Rightarrow {I_R} = {I_1} + {I_2} + 2\sqrt {{I_1}} \sqrt {{I_2}} $
The resultant intensity is nothing but the maximum intensity, that is ${I_{\max }}$.
The maximum intensity of the light is given as,
$ {I_{\max }} = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} $
$ \Rightarrow {I_{\max }} = 16 + 25 + 2\sqrt {16 \times 25} $
$ \Rightarrow {I_{\max }} = 16 + 25 + 2\sqrt {400} $
$ \Rightarrow {I_{\max }} = 16 + 25 + 2(20)$
$ \Rightarrow {I_{\max }} = 16 + 25 + 40$
Use addition to simplify the equation to get the maximum intensity.
$\therefore {I_{\max }} = 81$
The intensity of the light at one point is $81$.
Hence, the correct answer is option (D).
Note: The light sources that emit the light of same frequency, wavelength are known as coherent sources. Coherent sources are of two types. One is temporal coherence and another one is spatial coherence. When the superimposition of waves occurs, the coherent sources form sustained interference patterns.
Formula used:
The resultant intensity,
${I_R} = {I_1} + {I_2} + 2\sqrt {{I_1}} \sqrt {{I_2}} \cos \phi $
Where, $\phi = 0$.
To find the maximum intensity,
${I_{\max }} = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} $
Complete step by step answer:
In the question, it is given that the two coherent sources of equal intensity produce maximum intensity of $100$ units.
We can consider the Young’s double slit experiment for better understanding.

In this diagram, the intensities of the two sources are given and it is represented as $I$and$P$is the maximum intensity of $100\% $. The two sources have equal intensities.
We can consider the maximum intensity. The maximum intensity is given as,
$ {I_{\max }} = {(\sqrt {{I_1}} + \sqrt {{I_2}} )^2}$
We can simplify the given equation as
$ \Rightarrow {I_{\max }} = 2{(\sqrt I )^2}$
$ \Rightarrow 4I$
In the question it is given that maximum intensity $100$ and the intensity of one source is calculated as,
$ \Rightarrow I = \dfrac{{100}}{4}$
$ \Rightarrow I = 25$
We have calculated the intensities of the two coherent sources. The intensity value of one source is $25$. Both the intensities are equal and hence the value of another intensity is also $25$. We can represent these values in the given diagram.
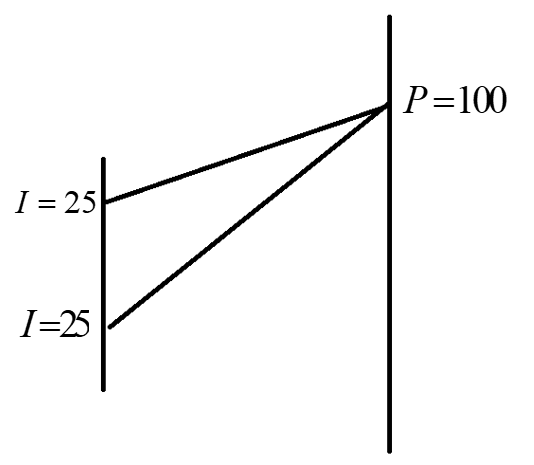
In the question they said that one of the intensities is reduced into $36$% of its width. We can consider the reduced intensity as new intensity that is ${I_{new}}$. Let us consider the ${I_1}$ as ${I_{new}}$.
$ \Rightarrow {I_{new}} = (25 - 25) \times \dfrac{{36}}{{100}}$
$ \Rightarrow 16$ units
Now we have the value of ${I_{new}}$ as $16$ units and ${I_2}$ as $25$. With the help of these values we can calculate the intensity of the light at the same point.
From the resultant intensity we can derive the formula for the maximum intensity. That is,
$ {I_R} = {I_1} + {I_2} + 2\sqrt {{I_1}} \sqrt {{I_2}} \cos \phi $
The value of $\cos \phi $ is $0$.
$ \Rightarrow {I_R} = {I_1} + {I_2} + 2\sqrt {{I_1}} \sqrt {{I_2}} $
The resultant intensity is nothing but the maximum intensity, that is ${I_{\max }}$.
The maximum intensity of the light is given as,
$ {I_{\max }} = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} $
$ \Rightarrow {I_{\max }} = 16 + 25 + 2\sqrt {16 \times 25} $
$ \Rightarrow {I_{\max }} = 16 + 25 + 2\sqrt {400} $
$ \Rightarrow {I_{\max }} = 16 + 25 + 2(20)$
$ \Rightarrow {I_{\max }} = 16 + 25 + 40$
Use addition to simplify the equation to get the maximum intensity.
$\therefore {I_{\max }} = 81$
The intensity of the light at one point is $81$.
Hence, the correct answer is option (D).
Note: The light sources that emit the light of same frequency, wavelength are known as coherent sources. Coherent sources are of two types. One is temporal coherence and another one is spatial coherence. When the superimposition of waves occurs, the coherent sources form sustained interference patterns.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




