Question

The two equal sides of an isosceles triangle with fixed base$b$are decreasing at the rate of$3cm$per second. How fast is the area decreasing when the two equal sides are equal to base?

Answer 1

Hint: First name the triangle and sides. Draw a perpendicular and find the area of the triangle. Use Pythagoras theorem and then differentiate the area of triangle. And then after differentiation and simplification put$x=b$you will get the answer.

Complete step-by-step answer:

The derivative is defined as the rate of change of one quantity with respect to another. In terms of functions, the rate of change of function is defined as $\dfrac{dy}{dx}=f(x)={{y}^{'}}$. The ratio of$\dfrac{dy}{dx}$ is used as one of the applications of derivatives in real life and in various aspects.

The concept of derivatives has been used in small scale and large scale. Whether it is a matter of change of temperature or rate of change of shapes and sizes of an object depending upon the conditions etc.

The concept of derivatives has been used in many ways.

So the above question is also related to the application of derivatives.

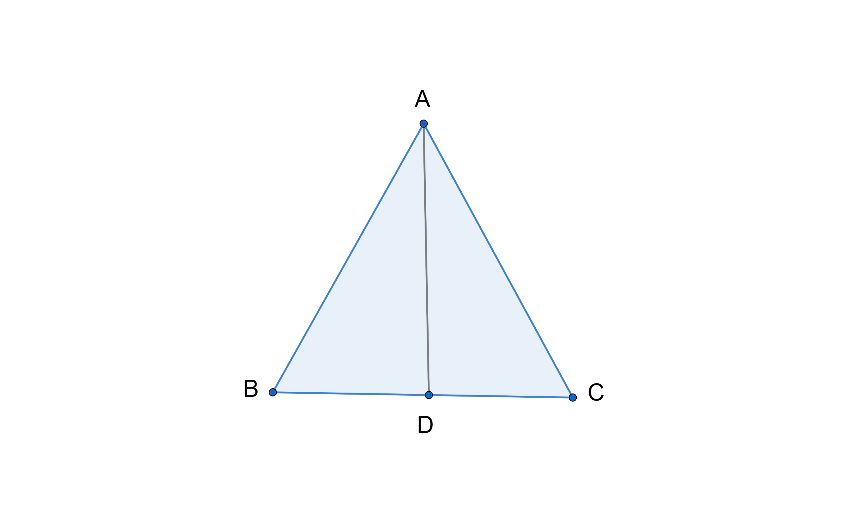
So now in question it is mentioned isosceles triangle so let us consider isosceles $\Delta ABC$,

So let$x$be the equal sides of $\Delta ABC$,

So$AB=AC=x$……………… (1)

So now$b$is the fixed base,

So$BC=b$

It is given in the question that the two equal sides of an isosceles triangle with fixed base$b$are decreasing at the rate of$3cm$per second.

i.e. $\dfrac{dx}{dt}=3cm$per second,

So it is mentioned in the question that we want to find how fast the area is decreasing when the two equal sides are equal to base i.e. $x=b$.

So in short we have to find$\dfrac{dA}{dt}$at$x=b$,

So for these we have to do construction, so the construction is as follows.

So draw a perpendicular $AD$to$BC$.

So we know the property of isosceles triangle that,

Perpendicular from vertex to side bisects the side that is , in simple words $D$is midpoint of$BC$.

So as $D$is midpoint of$BC$ so we get,

$BD=DC=\dfrac{BC}{2}$

Where$BC=b$,

So on whole we get,

$BD=DC=\dfrac{b}{2}$ ………….. (2)

Now considering $\Delta ADB$,

Using Pythagoras theorem,

${{(AB)}^{2}}={{(AD)}^{2}}+{{(BD)}^{2}}$

From (1) and (2), we get,

${{(x)}^{2}}={{(AD)}^{2}}+{{\left( \dfrac{b}{2} \right)}^{2}}$

So rearranging we get,

${{(AD)}^{2}}={{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}$

So simplifying in simple manner we get,

$AD=\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}$

We know that, Area of isosceles triangle$(A)=\dfrac{1}{2}\times base\times height$

So here $base=b$and$height=AD=\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2}

\right)}^{2}}}$

So substituting $base$and$height$we get,

$A=\dfrac{1}{2}\times b\times \sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}$

Now we want to find$\dfrac{dA}{dt}$so differentiating above we get,

$\dfrac{dA}{dt}=\dfrac{1}{2}\times b\times \dfrac{d\sqrt{{{\left( x \right)}^{2}}-{{\left(
\dfrac{b}{2} \right)}^{2}}}}{dt}$

So we know the differentiation of$\sqrt{x}$i.e.$\dfrac{d(\sqrt{x})}{dx}=\dfrac{1}{2\sqrt{x}}$.

So applying above, we get,

$\begin{align}

  & \dfrac{dA}{dt}=\dfrac{1}{2}\times b\left[ \dfrac{1}{2\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}}\times \dfrac{d\left( {{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}} \right)}{dt} \right] \\

 & \dfrac{dA}{dt}=\dfrac{1}{2}\times b\left[ \dfrac{1}{2\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}}\times \left( \dfrac{d({{x}^{2}})}{dt}-0 \right) \right] \\

\end{align}$

\[\dfrac{dA}{dt}=\dfrac{1}{2}\times b\left[ \dfrac{1}{2\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}}\times \left( \dfrac{d({{x}^{2}})}{dx}\times \dfrac{dx}{dt} \right) \right]\]

So simplifying we get,

\[\dfrac{dA}{dt}=\dfrac{1}{2}\times b\left[ \dfrac{1}{2\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}}\times \left( 2x\times \dfrac{dx}{dt} \right) \right]\]

So we know$\dfrac{dx}{dt}=3$, we get,

\[\dfrac{dA}{dt}=\left[ \dfrac{b}{4\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}}\times \left( 2x\times 3 \right) \right]\]

\[\dfrac{dA}{dt}=\left[ \dfrac{b}{4\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}}\times \left( 6x \right) \right]\]

\[\dfrac{dA}{dt}=\left[ \dfrac{6xb}{4\sqrt{{{\left( x \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}} \right]\]

Now we want to find$\dfrac{dA}{dt}$at$x=b$,

\[\dfrac{dA}{dt}=\left[ \dfrac{6{{b}^{2}}}{4\sqrt{{{\left( b \right)}^{2}}-{{\left( \dfrac{b}{2} \right)}^{2}}}} \right]\]

So simplifying in simple manner we get,

\[\dfrac{dA}{dt}=\left[ \dfrac{6{{b}^{2}}}{4\sqrt{{{b}^{2}}-\dfrac{{{b}^{2}}}{4}}} \right]\]

\[\dfrac{dA}{dt}=\left[ \dfrac{6{{b}^{2}}}{4\sqrt{\dfrac{3{{b}^{2}}}{4}}} \right]\]

\[\dfrac{dA}{dt}=\left[ \dfrac{3{{b}^{2}}}{\sqrt{3{{b}^{2}}}} \right]\]

\[\dfrac{dA}{dt}=\left[ \dfrac{3b}{\sqrt{3}} \right]\]

\[\dfrac{dA}{dt}=\left[ b\sqrt{3} \right]\]

So we get,

\[\dfrac{dA}{dt}=b\sqrt{3}\]

So the dimension of area is $c{{m}^{2}}$per second.

So we get the final answer of$\dfrac{dA}{dt}$at $x=b$is\[b\sqrt{3}c{{m}^{2}}\]per second.


So the area decreasing fast when the two equal sides are equal to base is\[b\sqrt{3}c{{m}^{2}}\]per second.

Note: read the question carefully. So you should know what is asked. Also you must know the assumption. So while differentiating confusion occurs, solve it in a simple way and don't get confused.

When there is substitution of so carefully see that if any term is missing.