
The unit of mobility is:
Answer
511.5k+ views
Hint:
Knowledge of the charge transport phenomenon in conductors is vital to solve this problem. Making a circuit diagram of the charge transport phenomenon will assist in solving this problem easily. Drift velocity
Step by step solution:
Let’s make a diagram of current flowing through a conductor to get an idea for the charge transport phenomenon in a conductor.
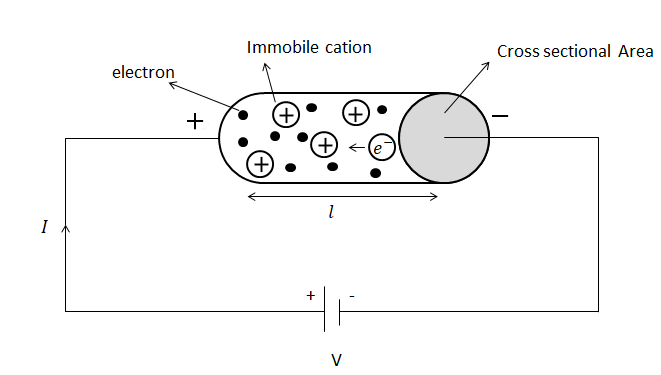
It is important to know as to why; we call the movement of electrons in the conductor from the negative end towards the positive end in the presence of an externally applied electric field as drift velocity and not just velocity of the electrons. It is known as drift velocity, because in the presence of no externally applied electric field, the electrons would still be randomly moving at high velocities, however upon the application of the electric field, the electrons start to get aligned as per the electric field, and the these electrons start to gain speed due to the applied field itself. These electrons hit with other electrons to transfer the momentum being generated, hence, giving an overall picture of the electron drifting through the conductor, leading to the name drift velocity. This whole phenomenon is known as charge transport phenomenon.
When a potential difference ‘V’ is applied as shown in the diagram, an electric field ‘E’ will be produced across the conductor from the positive terminal towards the negative terminal. The free electrons of the conductor travel in the opposite direction of the applied electric field. Hence, the electrons travel from the negative end of the conductor (as marked in the diagram) towards the positive end of the conductor (as marked in the diagram). The velocity with which these electrons travel is known as drift velocity of the electrons or just drift velocity of the conductor.
The actual definition of drift velocity
The velocity gained by these electrons is dependent only upon the externally applied Electric field (E). That is:
Since, the Electric field (E) is given by:
Hence, the unit of electron mobility will be:
Therefore, the Option (B) is the solution.
Note:
In the following solution, we consider the mobility to be called electron mobility denoted as
Further, these two values of mobility will always be positive, for both the electron and holes as major charge carriers of the conductor.
Knowledge of the charge transport phenomenon in conductors is vital to solve this problem. Making a circuit diagram of the charge transport phenomenon will assist in solving this problem easily. Drift velocity
Step by step solution:
Let’s make a diagram of current flowing through a conductor to get an idea for the charge transport phenomenon in a conductor.

It is important to know as to why; we call the movement of electrons in the conductor from the negative end towards the positive end in the presence of an externally applied electric field as drift velocity and not just velocity of the electrons. It is known as drift velocity, because in the presence of no externally applied electric field, the electrons would still be randomly moving at high velocities, however upon the application of the electric field, the electrons start to get aligned as per the electric field, and the these electrons start to gain speed due to the applied field itself. These electrons hit with other electrons to transfer the momentum being generated, hence, giving an overall picture of the electron drifting through the conductor, leading to the name drift velocity. This whole phenomenon is known as charge transport phenomenon.
When a potential difference ‘V’ is applied as shown in the diagram, an electric field ‘E’ will be produced across the conductor from the positive terminal towards the negative terminal. The free electrons of the conductor travel in the opposite direction of the applied electric field. Hence, the electrons travel from the negative end of the conductor (as marked in the diagram) towards the positive end of the conductor (as marked in the diagram). The velocity with which these electrons travel is known as drift velocity of the electrons or just drift velocity of the conductor.
The actual definition of drift velocity
The velocity gained by these electrons is dependent only upon the externally applied Electric field (E). That is:
Since, the Electric field (E) is given by:
Hence, the unit of electron mobility will be:
Therefore, the Option (B) is the solution.
Note:
In the following solution, we consider the mobility to be called electron mobility denoted as
Further, these two values of mobility will always be positive, for both the electron and holes as major charge carriers of the conductor.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




