Question

The value of$\cos \theta $ increases as $\theta $ increases. Enter 1 for true and 0 for false.

Answer 1

Hint: Look at the graph of cosine and check in the interval from 0 to 180. If the value of $\cos \theta $ increases as $\theta $ increases then the answer is 1 else it is 0.

Complete step-by-step answer:
For a right angled triangle, the ratio of the sides gives certain trigonometric functions.
$\cos \theta $is the ratio of the base and the perpendicular. So, $\cos \theta = \dfrac{b}{c}$.

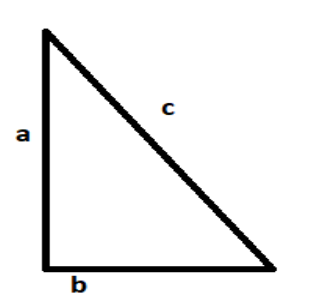
Similarly, one can get the other trigonometric ratios as well by taking different sets of sides.
For different angles, one can plot the variation of this function with the varying angle$\theta $.
The graph of $\cos \theta $looks like:

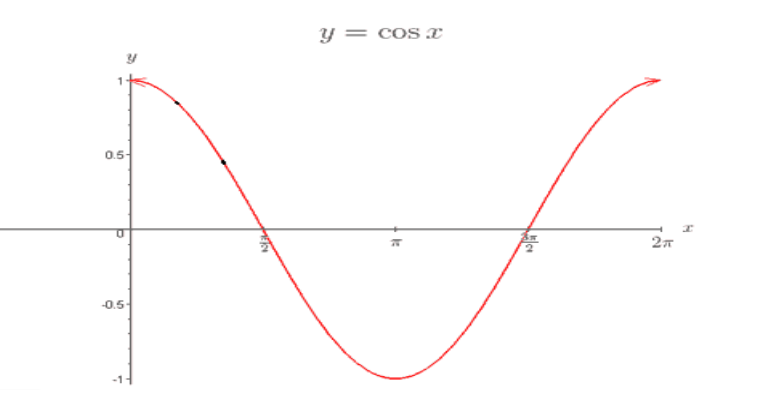
The cosine function has the following properties:
It is a decreasing function from 0 to 180.
It is symmetric about the y axis.
It has $2\pi $ as its period.
In the interval 0 to 90 we can see that as the angle $\theta $ is increasing the function $\cos \theta $ will decrease from 1 to 0 and on further going from 90 to 180 the function takes values from 0 to -1. So, it is clear from the graph that the cosine function decreases in the interval 0 to 180.
So, the correct answer is a false so we enter 0.

Note: Since no interval was mentioned in the question the standard domain of 0 to 180 was taken. Otherwise, the graph is a sinusoidal curve and is either decreasing or increasing, according to the interval.