Question

The velocity of efflux of a liquid through an orifice in the bottom of the tank does not depend upon:
A. Size of orifice.
B. Height of liquid
C. Acceleration due to gravity
D. Density of liquid

Answer 1

Hint: The velocity of efflux is explained by two theorems. Torricelli’s theorem and Bernoulli’s theorem. Torricelli's theorem tells that speed of efflux v of a fluid through a well-defined orifice at the bottom of a tank filled to a depth h is exactly as same as that of velocity of a body which is acquired when falling freely from a height h.

Formula used:
${{p}_{0}}+\dfrac{1}{2}{{\rho }_{b}}{{v}^{2}}={{p}_{0}}+{{\rho }_{l}}gh$

Complete answer:
First of all we should know about the velocity of efflux .It is explained by two theorems. Torricelli’s theorem and Bernoulli’s theorem. Torricelli's theorem tells that speed of efflux v of a fluid through a well-defined orifice at the bottom of a tank filled to a depth h is exactly the same as that of velocity of a body which is acquired when falling freely from a height h. According to Bernoulli’s theorem, it is given that,

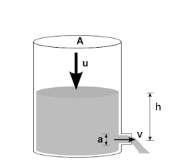
In which ${{\rho }_{b}}$ is the density of liquid at the bottom, v is the velocity of efflux, ${{p}_{0}}$ is the pressure, ${{\rho }_{l}}$ is the density of liquid, g is the acceleration due to gravity and h is the height of the liquid column. The density of the fluid is actually varying with height h. In certain times velocity of efflux depends on the density of the liquid also. And the velocity of efflux independent of the size of orifice.

So, the correct answer is “Option A”.

Note:
Bernoulli's equation is having great importance in solving this question. The formula used is
${{p}_{0}}+\dfrac{1}{2}{{\rho }_{b}}{{v}^{2}}={{p}_{0}}+{{\rho }_{l}}gh$
This has to be remembered well. The easiest form of Bernoulli's equation states that the sum of mechanical energy, potential energy and kinetic energy, along a streamline, is constant.