Question

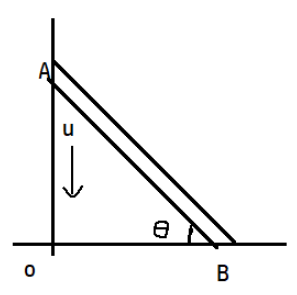
The velocity of end A of a rigid rod placed between two smooth vertical walls is u along the vertical direction. Find out the velocity of end B of that rod, rod always remains in contact with the vertical wall and also finds the velocity of the centre of the rod. Also, find the equation of path of the centre of the rod.

Answer 1

Hint:The point to be noted is that the ladder remains in contact with the floor and the wall during its entire motion. Also there is nothing mentioned about the composition of the weight so we assume that the composition is uniform throughout.

Complete step by step answer:
let OA= y and OB= x
considering triangle OAB, right-angled at O,
\[\begin{align}
&\Rightarrow \cos \theta =\dfrac{x}{AB} \\
&\Rightarrow x=AB\cos \theta \\
&\Rightarrow \sin \theta =\dfrac{y}{AB} \\
&\Rightarrow y=AB\sin \theta \\
\end{align}\]
The velocity of end A u will be given by the rate of change of y concerning time t.
Using calculus tools,
\[\begin{align}
&\Rightarrow y'=AB\cos \theta \dfrac{d\theta }{dt} \\
&\Rightarrow u=AB\cos \theta \dfrac{d\theta }{dt} \\
&\Rightarrow x'=-AB\sin \theta \dfrac{d\theta }{dt} \\
&\Rightarrow v=-AB\sin \theta \dfrac{d\theta }{dt} \\
\end{align}\]
Now, finding the value of;
\[\Rightarrow AB\dfrac{d\theta }{dt}\], \[\dfrac{u}{\cos \theta
}=AB\dfrac{d\theta }{dt}\]
We can put this value to find out v,
\[\begin{align}
&\Rightarrow v=-\sin \theta \times \dfrac{u}{\cos \theta } \\
&\Rightarrow v=-u\tan \theta \\
\end{align}\]
Thus, the velocity of end B of that rod is \[v=-u\tan \theta \].
Now, we need to find the equation of path of the centre of the rod. Let the Position of Centre of Mass of the rod be (p,q)
Since the rod composition is uniform its centre of mass will lie at its geometrical centre at half distance from any endpoint. Therefore (p,q) = \[(\dfrac{x}{2},\dfrac{y}{2})\]
The trajectory of the centre of mass can be written as then \[\Rightarrow(\dfrac{x}{2}\widehat{i}+\dfrac{y}{2}\widehat{j})\]
Now to find the velocity of the centre of mass we differentiate the trajectory equation,
\[\Rightarrow\dfrac{d(\dfrac{x}{2}\widehat{i}+\dfrac{y}{2}\widehat{j})}{dt}=\dfrac{1}{2}(x'+y')=\dfrac{1}{2}(u+v)\]
Now to find the magnitude, since velocity is a vector so,
\[\begin{align}
&\Rightarrow \left| {{v}_{g}} \right|=\dfrac{1}{2}\sqrt{{{u}^{2}}+{{v}^{2}}} \\
& \Rightarrow \left| {{v}_{g}} \right|=\dfrac{1}{2}\sqrt{{{(AB\cos \theta \dfrac{d\theta }{dt})}^{2}}+{{(-AB\sin \theta \dfrac{d\theta }{dt})}^{2}}} \\
& \Rightarrow \left| {{v}_{g}} \right| =\dfrac{1}{2}\sqrt{A{{B}^{2}}\dfrac{{{d}^{2}}\theta }{d{{t}^{2}}}} \\
& \Rightarrow \left| {{v}_{g}} \right|=\dfrac{AB}{2}\dfrac{d\theta }{dt} \\
& \\
\end{align}\]
Using \[\dfrac{u}{\cos \theta }=AB\dfrac{d\theta }{dt}\], we can write this as
\[{{v}_{g}}=\dfrac{u}{2\cos \theta }\]

Therefore, the velocity of the centre of the rod will be given by\[{{v}_{g}}=\dfrac{u}{2\cos \theta }\].

Note:While doing differentiation, we need to keep in mind that we are differentiating concerning time and not concerning the angle. Also, velocity is a vector and to find its magnitude we have its dot product with itself which is the easiest way to find the magnitude of any vector.