Question

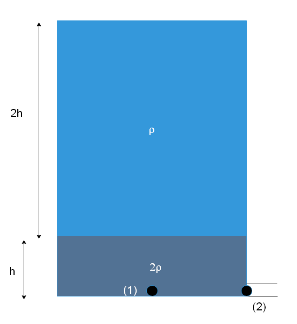
The velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities $2\rho $ and $\rho $ as shown in the figure is

A) $\sqrt {6gh} $
B) $2\sqrt {gh} $
C) $2\sqrt {2gh} $
D) $\sqrt {gh} $

Answer 1

Hint: Bernoulli’s theorem relates the pressure of a liquid at any point of the container due to any kind of fluid in it. We need to calculate the pressure due to gravity and the bottom of the liquid and equalize it with the pressure just outside the hole due to the flow of the water.

Formula used: In this solution we will be using the following equations
Bernoulli’s Equation:$P = {P_{atm}} + \rho gh + \dfrac{1}{2}\rho {v^2}$where $P$ is the pressure of the liquid at a certain point, ${P_{atm}}$ is the atmospheric pressure , $h$ is the height of the liquid of density $\rho $ below a reference point, and $v$ is the velocity of the liquid flow.

Complete step by step solution:
In the figure, at point (1), the pressure will be due to both kinds of fluids. Since both the fluids are stationary at point (1), we can calculate the pressure at that point using the Bernoulli’s theorem as:
$\Rightarrow{P_1} = {P_{atm}} + (\rho )g(2h) + (2\rho )g(h)$
So on calculating we get
$\Rightarrow{P_1} = {P_{atm}} + 4\rho gh$
At point (2), the fluid of density $2\rho $ is being thrown out of the container and will have a velocity $v$ and will be at atmospheric pressure so we can calculate the pressure at point (2) as
$\Rightarrow{P_2} = {P_{atm}} + \dfrac{1}{2}(2\rho ){v^2}$
Since the pressures at both the points should be equal from Bernoulli’s theorem, we can write
$\Rightarrow{P_1} = {P_2}$
So substituting we get,
$\Rightarrow{P_{atm}} + 4\rho gh = {P_{atm}} + \dfrac{1}{2}(2\rho ){v^2}$
Dividing both sides by $\rho $ and on cancelling ${P_{atm}}$ we get
$\Rightarrow{v^2} = 4gh$
On taking square root,
$v = 2\sqrt {gh} $ which corresponds to option (B).

Note:
Here we have assumed that the interface between the two fluids remains at a constant height and hence the pressure due to the volume of the liquids can be calculated easily. In reality, the interface would become diagonal and there could even be mixing of the two fluids depending on the dimensions of the container.