Question

The velocity-time graph of the particle moving along a straight line is shown. The rate of acceleration and deceleration is constant and it is equal to $5m{{s}^{-2}}$. If the average velocity during the motion is $20m{{s}^{-1}}$, then find the value of t.

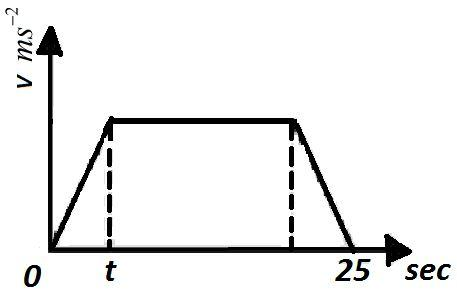
A. 6s
B. 5s
C. 9s
D. 4s

Answer 1

Hint: Since the body’s change in velocity for both acceleration and deceleration are the same, time taken (t) should be also the same for acceleration and deceleration to be equal. Also, recall that the area under a velocity time graph gives displacement. We could also get the value of displacement from the product of total time taken and average velocity and then equate the same to the area and hence find time t from the quadratic equation so formed.

Formula used:
$\overline{v}=\dfrac{\Delta x}{\Delta t}$
Newton’s first law of motion,
$v=u+at$

Complete step-by-step answer:
Let us recall the definition of average velocity.
Average velocity is the total change in position (or simply, the displacement) in the given time interval. That is,
$\overline{v}=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}}$
$\overline{v}=\dfrac{\Delta x}{\Delta t}$
We are given the average velocity of the body in the question,
$\overline{v}=20m{{s}^{-1}}$
Also, the time taken for the displacement to take place is $\Delta t=25s$ .
So, we get the displacement as their product, that is,
$\Delta x=\overline{v}\times \Delta t=20\times 25=500m$ …………….. (1)

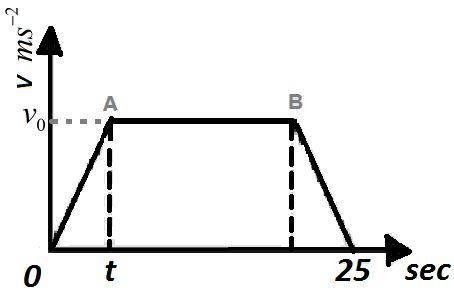
We are given that the rate of acceleration= the rate of deceleration=$5m{{s}^{-2}}$ ……………. (2)
Also, we know that during acceleration velocity is changed from 0 to ${{v}_{0}}$ and during deceleration it is changed back to 0 from ${{v}_{0}}$ . Now, condition (2) can only be satisfied if time taken for acceleration and deceleration is the same=t. Therefore, the duration A to B, when the body travels with constant velocity can now be given by,
${{t}_{AB}}=25-2t$ ……………. (3)
From Newton’s first law of motion we have,
$v=u+at$ ……………… (4)
We know that initial velocity (u) =0,
Final velocity (v) =${{v}_{0}}$
$a=5m{{s}^{-2}}$
So, (4) gives,
${{v}_{0}}=5t$ ………………. (5)
We are given a velocity-time graph in the question and we know that area under a velocity-time graph gives us the displacement of the body.
Area under the given graph =displacement (∆x) = 2(area of the triangular part) + area of the rectangular part
$\Delta x=2\left( \dfrac{1}{2}\times t\times {{v}_{0}} \right)+({{t}_{AB}}\times {{v}_{0}})$
Substituting for $\Delta x$, ${{t}_{AB}}$ and${{v}_{0}}$ from (1), (3) and (5) respectively, we get,
$500=2\left( \dfrac{1}{2}\times t\times 5t \right)+\left( 25-2t \right)5t$
${{t}^{2}}-25t+100=0$
$\left( t-20 \right)\left( t-5 \right)=0$
This quadratic equation has two solutions, t=5 and t=20,
Since, 2t should definitely be less than 25, t=5s.
So, the correct answer is “Option B”.

Note: In questions like this with graphical representation of motion, the graph itself carries a lot of information that is required to solve the question. We should be able to extract all the information available from the graph, for which conceptual clarity is a must. For example, if you did not know that area under the given graph gives the displacement, you will reach nowhere near the answer even with all the other given values.