Question

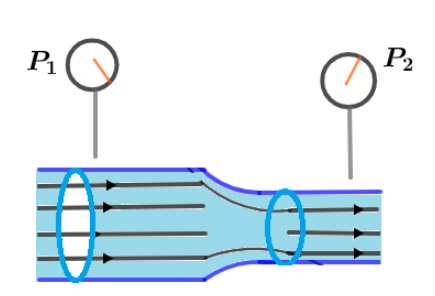
The venture tube as shown in the figure is used as a fluid meter. Suppose the device is used at a service station to measure the flow rate of gasoline ( $\rho = 7.0 \times {10^2}\,kg{m^{ - 3}}$ ) through a hose having outlets radius of $1.20\,cm$ . If the difference in pressure is measured as ${P_1} - {P_2} = 1.2\,kPa$ and the radius of inlet is $2.40\,cm$.Find the speed of the gasoline as it leaves the hose.

Answer 1

Hint: In order to solve the given question, we will use the concept of venture effect of fluids which states that, there always gets a reduction in fluid pressure when fluid passes through a choke or constricted section of a pipe and the relation between pressures is given as ${P_1} - {P_2} = \dfrac{\rho }{2}({v_2}^2 - {v_1}^2)$.

Formula used:
Rate of flow of fluid through a circular section at both ends of a venturi meter is constant and written as,
$\pi {r_1}^2{v_1} = \pi {r_2}^2{v_2}$
where, ${r_1},{r_2}$ are the radii of inlet and outlet circular ends of the pipe.

Complete step by step answer:
Let us first find the velocity relation from given parameters using the relation of rate of flow, $\pi {r_1}^2{v_1} = \pi {r_2}^2{v_2}$ .
Given that, ${r_1} = 2.40cm$ and ${r_2} = 1.20\,cm$ put these values in equation $\pi {r_1}^2{v_1} = \pi {r_2}^2{v_2}$ we get,
${(2.4)^2}{v_1} = {(1.2)^2}{v_2}$
$\Rightarrow {v_2} = 4{v_1} \to (i)$
Now, using the venturi effect formula, ${P_1} - {P_2} = \dfrac{\rho }{2}({v_2}^2 - {v_1}^2)$ we have given that,
${P_1} - {P_2} = 1.2kPa$
$\Rightarrow \rho = 7.0 \times {10^2}kg{m^{ - 3}}$
And put value of ${v_2} = 4{v_1}$ we get,
${P_1} - {P_2} = \dfrac{\rho }{2}({v_2}^2 - {v_1}^2)$
$\Rightarrow 1.2 \times {10^3} = \dfrac{{7.0 \times {{10}^2}}}{2}(16{v_1}^2 - {v_1}^2)$
$\Rightarrow \dfrac{{24}}{7} = 15{v_1}^2$
$\Rightarrow 0.0519 = {v_1}^2$
$\Rightarrow {v_1} = 0.228\,m\,{\sec ^{ - 1}}$
So from the relation ${v_2} = 4{v_1}$ the outlet velocity of fluid is
${v_2} = 4 \times 0.228$
$\therefore {v_2} = 1.91\,m\,{\sec ^{ - 1}}$

Hence, the velocity at which gasoline leaving hose is ${v_2} = 1.91\,m{\sec ^{ - 1}}$.

Note: It should be remembered that, Venturi meter is a device which is used to determine the rate of flow of a fluid through a pipe and rate of flow is taken as product of area of cross section of pipe and the velocity at which it enters, the basic unit of conversion must be remembered as $1kPa = {10^3}Pa$ .