
The voltage-current $ \left( {V - I} \right) $ graph of a metallic conductor at two different temperatures $ {T_1} $ and $ {T_2} $ is shown below. At which temperature is the resistance higher?

Answer
567.3k+ views
Hint: We need to state Ohm’s Law along with its formula. Using the formula for the Ohm’s law, we can find the line which has a greater slope to solve this problem.
Formula used: The following formulas are used to solve this question.
$ R = \dfrac{V}{I} $ where $ R $ is the resistance, $ V $ is the potential difference and $ I $ is the current.
Complete step by step solution:
According to Ohm’s Law, potential difference across a metallic conductor is proportional to the current flowing through it. This statement requires all physical conditions and temperature to remain constant.
$ V\alpha I $ where $ V $ is the potential difference and $ I $ is the current.
It can be written that, $ V = IR $ where $ R $ is the resistance, $ V $ is the potential difference and $ I $ is the current.
$ \Rightarrow R = \dfrac{V}{I} $ .
Now the graph for $ V $ against $ I $ shall be a straight line since they are directly proportional, but the proportionality constant $ R $ is different for the same conductors at the same temperature.
For a straight line in the X-Y coordinate axis, the slope of the line is given by,
Slope $ m = \dfrac{{\Delta y}}{{\Delta x}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $ where $ {{\text{y}}_{\text{2}}} $ and $ {{\text{y}}_{\text{1}}} $ are two points on the $ y $ -axis while, $ {x_2} $ and $ {x_1} $ are two points on the $ x $ -axis.
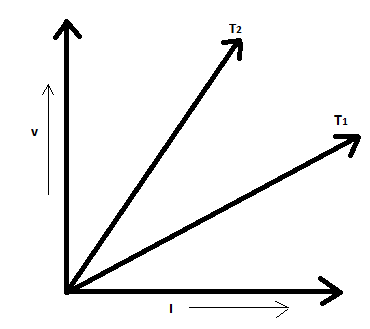
In the given figure, the voltage $ V $ and current $ I $ graph for a conductor at two different temperatures $ {T_1} $ and $ {T_2} $ are shown.
The value of slope of the lines will be given the formula,
$ m = \dfrac{{\Delta V}}{{\Delta I}} $ .
As said earlier, according to Ohm’s Law,
$ \dfrac{{\Delta V}}{{\Delta I}} = R $ where $ R $ is the resistance.
Thus, the slope of the line is equal to its resistance.
$ \therefore $ The resistance of the conductor will be higher for the curve which has a greater slope. Since the $ {T_1} $ curve has a greater slope, it has greater resistance.
Note:
Ohm's law is an empirical relation which accurately describes the conductivity of the vast majority of electrically conductive materials over many orders of magnitude of current.
However some materials, such as computers, telephones, do not obey Ohm's law, these are called non-Ohmic.
Formula used: The following formulas are used to solve this question.
$ R = \dfrac{V}{I} $ where $ R $ is the resistance, $ V $ is the potential difference and $ I $ is the current.
Complete step by step solution:
According to Ohm’s Law, potential difference across a metallic conductor is proportional to the current flowing through it. This statement requires all physical conditions and temperature to remain constant.
$ V\alpha I $ where $ V $ is the potential difference and $ I $ is the current.
It can be written that, $ V = IR $ where $ R $ is the resistance, $ V $ is the potential difference and $ I $ is the current.
$ \Rightarrow R = \dfrac{V}{I} $ .
Now the graph for $ V $ against $ I $ shall be a straight line since they are directly proportional, but the proportionality constant $ R $ is different for the same conductors at the same temperature.
For a straight line in the X-Y coordinate axis, the slope of the line is given by,
Slope $ m = \dfrac{{\Delta y}}{{\Delta x}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $ where $ {{\text{y}}_{\text{2}}} $ and $ {{\text{y}}_{\text{1}}} $ are two points on the $ y $ -axis while, $ {x_2} $ and $ {x_1} $ are two points on the $ x $ -axis.

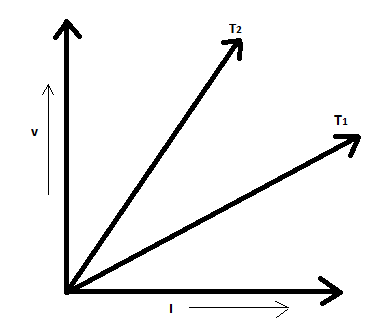
In the given figure, the voltage $ V $ and current $ I $ graph for a conductor at two different temperatures $ {T_1} $ and $ {T_2} $ are shown.
The value of slope of the lines will be given the formula,
$ m = \dfrac{{\Delta V}}{{\Delta I}} $ .
As said earlier, according to Ohm’s Law,
$ \dfrac{{\Delta V}}{{\Delta I}} = R $ where $ R $ is the resistance.
Thus, the slope of the line is equal to its resistance.
$ \therefore $ The resistance of the conductor will be higher for the curve which has a greater slope. Since the $ {T_1} $ curve has a greater slope, it has greater resistance.
Note:
Ohm's law is an empirical relation which accurately describes the conductivity of the vast majority of electrically conductive materials over many orders of magnitude of current.
However some materials, such as computers, telephones, do not obey Ohm's law, these are called non-Ohmic.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




