Question

The volume and curved surface area of the cylinder are 1650 cubic cm and 660 sq. cm respectively. Find the radius and height of the cylinder.

Answer 1

Hint: Let us assume the radius and height of the cylinder as ‘r’ and h respectively. We have given the volume and curved surface area of the cylinder. We know that the formula for the volume of the cylinder is $\pi {{r}^{2}}h$ and the formula for the curved surface area is $2\pi rh$. Now, equating the volume and curved surface area that we have just mentioned to 1650 and 660. Now, we have two equations and two unknowns so we can find the value of r and h.

Complete step-by-step solution:
We have given the volume and curved surface area of the cylinder as 1650 cubic cm and 660 sq. cm respectively.
Let us assume that the radius and height of the cylinder are r and h respectively.
In the below diagram, we have shown a cylinder with radius (r) and height (h).

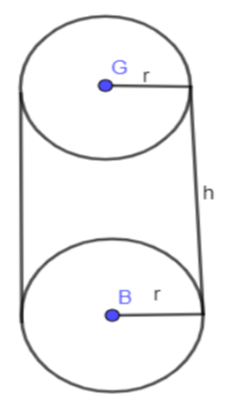
We know the formula for volume of the cylinder is equal to:
$\pi {{r}^{2}}h$
Equating the above volume to 1650 we get,
$\pi {{r}^{2}}h=1650$……… Eq. (1)
We know the formula for curved surface area of the cylinder is:
$2\pi rh$
Equating the above curved surface area to 660 we get,
$2\pi rh=660$…………. Eq. (2)
Now, we have two equations and two unknowns r and h which we are going to solve by dividing eq. (1) by eq. (2).
$\dfrac{\pi {{r}^{2}}h}{2\pi rh}=\dfrac{1650}{660}$
In the above equation, $\pi ,r,h$ will be cancelled out from the numerator and the denominator we get,
$\dfrac{r}{2}=\dfrac{165}{66}$
Multiplying 2 on both the sides we get
$\begin{align}
  & r=\dfrac{165\times 2}{66}=\dfrac{330}{66} \\
 & \Rightarrow r=5cm \\
\end{align}$
Substituting the above value of r in eq. (2) we get,
$2\pi \left( 5 \right)h=660$
Substituting the value of $\pi $ as $\dfrac{22}{7}$ in the above equation we get,
$\begin{align}
  & 2\left( \dfrac{22}{7} \right)\left( 5 \right)h=660 \\
 & \Rightarrow \dfrac{220}{7}h=660 \\
\end{align}$
Cross multiplying the above equation we get,
$\begin{align}
  & 220h=660\left( 7 \right) \\
 & \Rightarrow 220h=4620 \\
 & \Rightarrow h=\dfrac{4620}{220} \\
 & \Rightarrow h=21cm \\
\end{align}$
Hence, we have got the value of radius (r) as 5 cm and height (h) as 21 cm.

Note: You can verify that the value of the radius and height of the cylinder that you solved above is correct or not by substituting these values in the formula of the curved surface area of the cylinder.
The formula of curved surface area for cylinder is equal to:
$2\pi rh$
Substituting the value of r and h as 5 cm and 21 cm respectively in the above equation we get,
$2\left( \dfrac{22}{7} \right)\left( 5 \right)\left( 21 \right)$
21 will be cancelled out 3 times by 7 in the above expression and we get,
$\begin{align}
  & 2\left( 22 \right)\left( 5 \right)\left( 3 \right) \\
 & =660c{{m}^{2}} \\
\end{align}$
Now, as you can see in the question given above, the curved surface area of the cylinder is $660c{{m}^{2}}$ which is matching with the value of curved surface area that we have just calculated by putting r and h as 5cm and 21 cm respectively.
Hence, the value of the radius and height of the cylinder that we are getting is correct.