Question

There are two set-squares in your box. What are the measures of the angles that are formed at the corners? Do they have any angle whose measurement is common?

Answer 1

Hint: First take one set-square and note the measurement of its angles and then take the other set-square and note its measurement. Now, check that is there any angle whose measurement is common in both the set squares.

Complete step-by-step answer:
Given that there are two set-square in the box.
The goal of the problem is to find the angles that are formed at the corners and then determine that measurement of any of the angles is common in both the set-squares.
Take a look at the figure of first set-square:

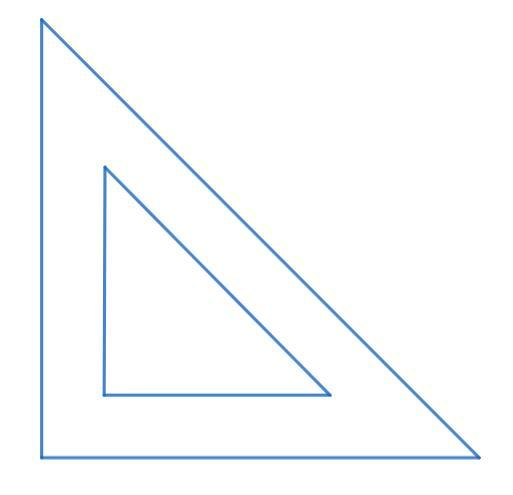
This is the right-angled triangle so one of its angles is $90^\circ $and the other two angles are equal in measure and have a measure of $45^\circ $. So, the measurements of the first set-square are:
$90^\circ ,45^\circ $ and $45^\circ $.
Now, take a look at the figure of other set-square:

This is also the right-angled triangle so one of its angles is $90^\circ $ and the other two angles of the set square are $30^\circ $ and$60^\circ $. Then the measurements of the second set-square are:
$90^\circ ,60^\circ $and$30^\circ $.
So, the measurement of the set -squares are given as:
1st set square- $90^\circ ,45^\circ $and$45^\circ $.
2nd set square- $90^\circ ,60^\circ $and$30^\circ $.

Yes, they have an angle whose measurement is common in both the set-square.
It can be seen in both the set squares that they are right-angled triangles so one of the angles in both the set-square have the common measure and the measurement of the common measure is $90^\circ $.

Note: Both the set-square are the right-angled triangle, so one of the angles in both the triangles has the measurement of$90^\circ $. So, both the set-square have a common angle.