
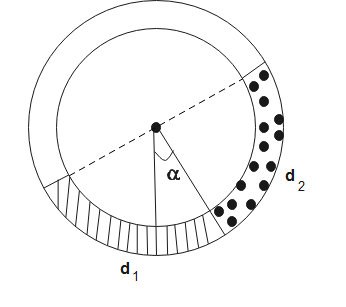
There is a circular tube in a vertical plane. Two liquids which do not mix and are of densities
(A).
(B).
(C).
(D).

Answer
476.7k+ views
Hint: Two liquids of densities do not mix with each other and are at equilibrium at the interface. Using Bernoulli’s equation, we can calculate the pressure of each liquid. As they are at equilibrium at the interface, pressure due to both liquids will be equal and opposite.
Formulas Used:
Complete answer:
Given two liquids of density
At the interface, both liquids are at equilibrium. Therefore, the pressure due to both liquids is equal at the interface.
According to Bernoulli’s theorem, the pressure due to liquids is-
Here,
For liquid-1,
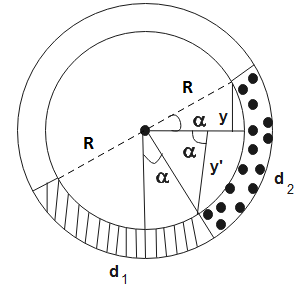
From the figure, we can see that,
So the height of liquid with density
From eq (1), the pressure of liquid will be-
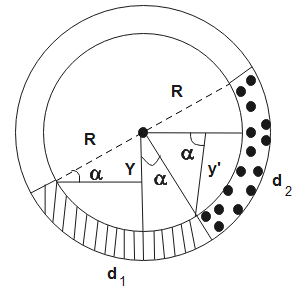
Form the above figure, we can see that,
So the height of liquid with density
From eq (1), the pressure of the liquid is-
At the interface pressure is same, therefore equating eq (2) and eq (3), we get,
Dividing the above equation by
The ratio of
Hence, the correct option is (A).
Note:
Pressure due to a fluid is the force exerted by it per unit area. A fluid enclosed in a container exerts pressure in all the directions. Bernoulli’s principle says that when the velocity of fluid increases, its potential energy decreases. Bernoulli's principle follows the law of conservation of energy, i.e. sum of all energies possessed by the flowing fluid is constant.
Formulas Used:
Complete answer:
Given two liquids of density
At the interface, both liquids are at equilibrium. Therefore, the pressure due to both liquids is equal at the interface.
According to Bernoulli’s theorem, the pressure due to liquids is-
Here,
For liquid-1,

From the figure, we can see that,
So the height of liquid with density
From eq (1), the pressure of liquid will be-

Form the above figure, we can see that,
So the height of liquid with density
From eq (1), the pressure of the liquid is-
At the interface pressure is same, therefore equating eq (2) and eq (3), we get,
Dividing the above equation by
The ratio of
Hence, the correct option is (A).
Note:
Pressure due to a fluid is the force exerted by it per unit area. A fluid enclosed in a container exerts pressure in all the directions. Bernoulli’s principle says that when the velocity of fluid increases, its potential energy decreases. Bernoulli's principle follows the law of conservation of energy, i.e. sum of all energies possessed by the flowing fluid is constant.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the difference between resemblance and sem class 12 social science CBSE




