Question

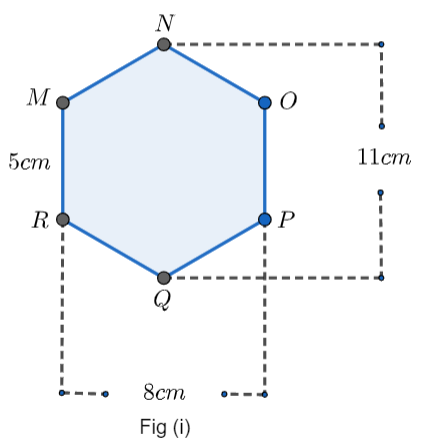
 There is a hexagon MNOPQR of each side 5cm and symmetric about NQ. Suresh and Rushika divided it into different ways. Find the area of this hexagon using both ways.

Answer 1

Hint: In Suresh’s case, the hexagon is divided into two trapeziums. Use the formula for the area of trapezium to find the area of each part. Then add both to find the area of the hexagon. In Rushika’s case, the hexagon is divided into two triangles and a rectangle. Find the area of each part and add them to get the area of the entire hexagon.

Complete step by step answer:
 In the figure, we are given a hexagon MNOPQR of each side 5cm. Also, the length between the point N and the point Q is given to be 11cm and the distance between the parallel sides MR and OP are 8cm.
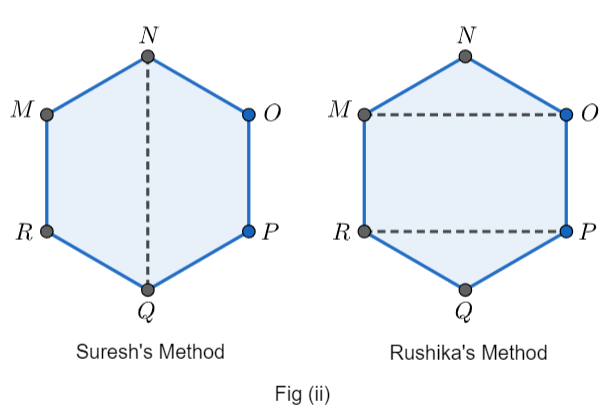
In Suresh’s Method, we can see that he has divided the given hexagon into two parts about the line NQ. Also, it is given in the question that the hexagon MNOPQR is symmetric about the line NQ.
So, by observation, we can see that it has resulted in the formation of two trapeziums of equal areas. These are NOPQ and NMRQ. So, let us first find the area of one of them.
Let us consider the Trapezium NOPQ:
We know that the area of a trapezium = $\dfrac{1}{2}\times (Sum)\times (Height)$
Here, the sum is the sum of the lengths of the two parallel sides i.e. NQ and OP. And, height is the distance between these two parallel sides.
So, NQ = 11cm (it is given in the question) OP = 5cm (it is given in the question)
Therefore, Sum = NQ + OP = 11+5 = 16cm.
As the distance between the parallel sides MR and OP is 8cm, therefore, the distance between the sides, NQ and OP will be 4cm (as it is symmetric about the line NQ)
So, the area of the trapezium is $\begin{align}
  & \dfrac{1}{2}\times (Sum)\times (Height) \\
 & \Rightarrow \dfrac{1}{2}\times (16)\times (4)=32 \\
\end{align}$
Hence, the area of the trapezium is 32 sq.cm.
Hence, using Suresh’s Method, the area of the given hexagon will be 32x2 = 64 sq.cm
Now, in Rushika’s method, we can see that she has joined the vertex M with the vertex O and also, the vertex R with the vertex P. This has resulted in the formation of one rectangle i.e. MOPR and two triangles of equal areas i.e. NMO and QRP.
So, let us first find the area of the rectangle MOPR.
We know, that the area of a rectangle = Length x Breadth
Here, length = MO = 8cm and breadth = OP = 5cm
Hence, the area of the rectangle MOPR = 8 x 5 = 40 sq.cm
Now, the area of the triangle NMO = the area of the triangle QRP = $\dfrac{1}{2}\times base\times height$
Here, base = MO = 8cm and height = $\dfrac{NQ-OP}{2}=\dfrac{11-5}{2}=\dfrac{6}{2}=3$ cm
Hence, the area of the triangle is $\dfrac{1}{2}\times 8\times 3=12$ sq.cm
Hence, the area of the given hexagon by Rushika’s method is = area of the rectangle MOPR + the area of the triangle NMO + the area of the triangle QRP = 40+12+12 = 64sq.cm
Note: The chances of mistakes can be in the calculation part and also, it can be committed while observing or following the particular concept or formula involved in the question which may result in the wrong answer.