Question

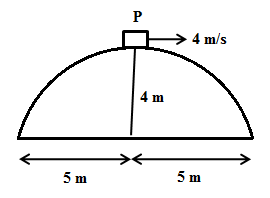
There is a parabolic shaped bridge across the width of 10 m. The highest point of the bridge is 4 m above the level of the bank. A car of mass 952 kg is crossing the bridge at a constant speed of 4 m/s. Find the force (in Newton) exerted on the bridge by car when it is at the highest point ‘P’ of the bridge. (take \[g = 10\,m/{s^2}\])

Answer 1

Hint: The net force exerted by the car on the bridge is the normal force provided by the bridge in the opposite direction. Draw the free body diagram and determine the value of normal force. Consider the effect of centrifugal force on the car to determine the net force.

Complete step by step solution:
We know that when a body moves in the circular motion, at each point, the centrifugal force acts on the body. The magnitude of this centrifugal force is the same as the centripetal force but it has the opposite direction.
We know that the force exerted by the car on the bridge is the normal force provided by the surface of the bridge. At the highest point, the weight of the car will be reduced due to centrifugal force.
At point P, the net force acting on the body is can be shown by drawing the free body diagram as shown in the figure below,

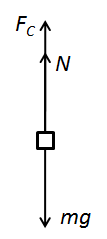
In the above figure, \[{F_C}\] is the centrifugal force, N is the normal force due to the surface of the bridge and m is the mass of the car.
Applying Newton’s second law of motion for the above free body diagram, we get,
\[{F_C} + N - mg = 0\]
\[ \Rightarrow N = mg - {F_C}\] ……. (1)
We know the centripetal force is given as,
\[{F_C} = \dfrac{{m{v^2}}}{R}\]
Here, v is the velocity of the car at position P and R is the radius of the semicircle shown in the figure.
Substituting the above equation in equation (1), we get,
\[N = mg - \dfrac{{m{v^2}}}{R}\]
\[ \Rightarrow N = m\left( {g - \dfrac{{{v^2}}}{R}} \right)\]
Substituting 952 kg for m, \[10\,m/{s^2}\] for g, 4 m/s for v and 4 m for R in the above equation, we get,
\[N = \left( {952} \right)\left( {10 - \dfrac{{{{\left( 4 \right)}^2}}}{4}} \right)\]
\[ \Rightarrow N = \left( {952} \right)\left( 6 \right)\]
\[ \Rightarrow N = 5712\,{\text{N}}\]

Therefore, the force exerted by the car on the bridge is 5712 N.

Note:
While drawing the free body diagram, make sure that the direction of centrifugal force is towards upward that is away from the centre of circular motion. While answering these types of questions, remember, the net force exerted on the ground is equal to the normal force provided by the ground and not just the weight of the body.