Question

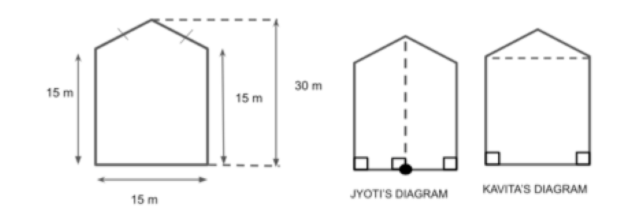
There is a pentagonal shaped park as shown in figure. For finding its area jyoti and kavita divided it into two different ways. Find the area of the park using both the ways.

Answer 1

Hint: Here, we will first use the symmetry principle, the area of trapezium BCDF is equal to area of trapezium BAEF, \[{\text{Area of pentagon ABCDE}} = 2 \times {\text{Area of trapezium BCDF}}\], which we will find using the formula of a trapezium is \[\dfrac{1}{2} \times {\text{Sum of parallel sides}} \times {\text{Height}}\] from the diagram. Then we will find the area of pentagon ABCDE by adding the area of triangle ABC, where \[{\text{Area}} = \dfrac{1}{2} \times {\text{Base}} \times {\text{Height}}\] and area of square ACED, \[{\left( {{\text{side}}} \right)^2}\].

Complete step-by-step answer:
First, we will find the area of the jyoti’s diagram.

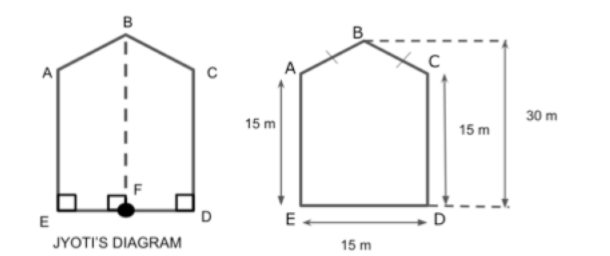
We know the area of pentagon ABCDE by adding the area of trapezium BCDF and area of trapezium BAEF.

Using the symmetry principle, the area of trapezium BCDF is equal to area of trapezium BAEF, we get
\[ \Rightarrow {\text{Area of pentagon ABCDE}} = 2 \times {\text{Area of trapezium BCDF}}\]
We know that in a trapezium BCDF, BF and CD are parallel sides, where DF is height.
Thus, we have from the given diagram.
\[ \Rightarrow {\text{BF}} = 30{\text{ m}}\]
\[ \Rightarrow {\text{CD}} = 15{\text{ m}}\]
\[
   \Rightarrow {\text{DF}} = \dfrac{{{\text{DE}}}}{2} \\
   \Rightarrow {\text{DF}} = \dfrac{{15}}{2}{\text{ m}} \\
 \]
We will know use the formula of a trapezium is \[\dfrac{1}{2} \times {\text{Sum of parallel sides}} \times {\text{Height}}\] from the above values, we get
\[ \Rightarrow {\text{Area of trapezium BCDF}} = \dfrac{1}{2} \times \left( {{\text{BF}} + {\text{CD}}} \right) \times {\text{DF}}\]
Substituting the values of BF, CD and DF in the above values, we get
\[
   \Rightarrow {\text{Area of trapezium BCDF}} = \dfrac{1}{2} \times \left( {30 + 15} \right) \times \dfrac{{15}}{2} \\
   \Rightarrow {\text{Area of trapezium BCDF}} = \dfrac{1}{2} \times 45 \times \dfrac{{15}}{2} \\
   \Rightarrow {\text{Area of trapezium BCDF}} = \dfrac{{45 \times 15}}{4} \\
 \]
Multiplying the above equation by 2 to find the area of pentagon ABCDE, we get
\[
   \Rightarrow {\text{Area of pentagon ABCDE}} = 2 \times \dfrac{{45 \times 15}}{4} \\
   \Rightarrow {\text{Area of pentagon ABCDE}} = \dfrac{{675}}{2} \\
   \Rightarrow {\text{Area of pentagon ABCDE}} = 337.5{\text{ }}{{\text{m}}^2} \\
 \]
Thus, the area of pentagon ABCDE is \[337.5{\text{ }}{{\text{m}}^2}\].
Now, we will find the area of the Kavita’s diagram.

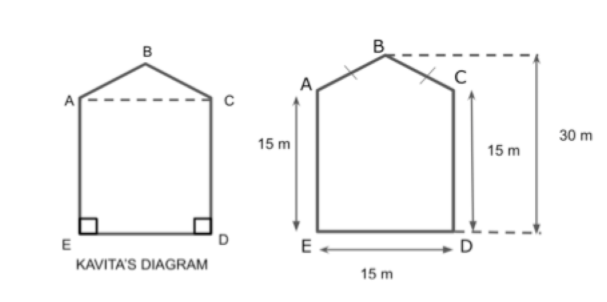
We know the area of pentagon ABCDE by adding the area of triangle ABC and area of square ACED.
Finding the area of triangle ABC using the formula of area of triangle \[{\text{Area}} = \dfrac{1}{2} \times {\text{Base}} \times {\text{Height}}\].
We know that the base of the triangle AC is 15 m.
Finding the height of the triangle from the above figure by subtracting the line CD from BD, we get
\[
   \Rightarrow 30 - 15 \\
   \Rightarrow 15{\text{ m}} \\
 \]
We will know use the formula of a triangle is \[\dfrac{1}{2} \times {\text{Base}} \times {\text{Height}}\] from the above values, we get
\[
   \Rightarrow {\text{Area}} = \dfrac{1}{2} \times 15 \times 15 \\
   \Rightarrow {\text{Area}} = \dfrac{{225}}{2} \\
   \Rightarrow {\text{Area}} = 112.5{\text{ }}{{\text{m}}^2} \\
 \]

Using the symmetry principle, ACDE is a square with side 15 m.

Using the formula of area of square ACDE is \[{\left( {{\text{side}}} \right)^2}\], we get
\[
   \Rightarrow {\text{Area of square ACDE}} = {15^2} \\
   \Rightarrow {\text{Area of square ACDE}} = 225{\text{ }}{{\text{m}}^2} \\
 \]
Thus, now we will find the area of pentagon ABCDE by adding the area of triangle ABC with area of square, we get
\[
   \Rightarrow {\text{Area of pentagon ABCDE}} = 112.5 + 225 \\
   \Rightarrow {\text{Area of pentagon ABCDE}} = 337.5{\text{ }}{{\text{m}}^2} \\
 \]
Thus, the area of pentagon ABCDE is \[337.5{\text{ }}{{\text{m}}^2}\].

Note: While solving these types of questions, students should know the formulas of area of trapezium and area of pentagon. We need to use the symmetry principle to decrease calculations. The only key part to solve this problem is to remember the basic formulae of areas of the shapes to ease the solution. Do not forget to write the units properly. Avoid calculation mistakes.