Question

Three blocks ${m_1} = 3kg,{m_2} = 2kg,{m_3} = 5kg$ lie on an inclined frictionless surface with inclination of 30 degree as shown in the figure.

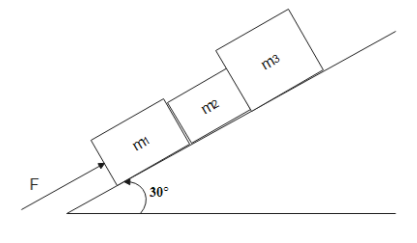
(a) what force(F) parallel to incline is needed to push the blocks up the plane with an acceleration $a = 2m/{s^2}$
(b) Find the contact force between ${m_1}$ and ${m_2}$ and between ${m_2}$ and ${m_3}$

Answer 1

Hint: This question can be answered by using newton’s second law. According to Newton's second law for a particular system rate of change of momentum will be equal to the external force acting on the system. Here external force will be responsible for the resulting acceleration of the system
Formula used:
${F_{ext}} = ma$

Complete answer:
According to Newton's second law the unbalanced external force will be responsible for the acceleration of the system. By seeing the diagram below we can interpret important information.

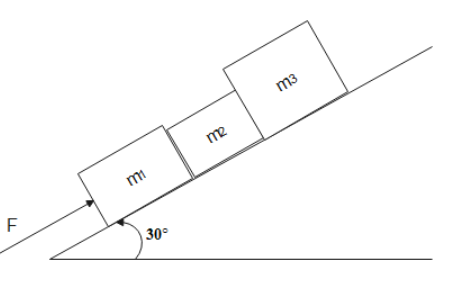
There will be weight of the blocks acting in the downward direction. If we resolve the weight of the blocks into components, we will get one component along the plane and another component perpendicular to the plane. We have the equation ${F_{ext}} = ma$
Along the plane the weight component will be$\left( {{m_1} + {m_2} + {m_3}} \right)g\sin \theta $
Where theta is the angle at which the plane is inclined with the horizontal which is 30 degrees here.
We need acceleration up the incline as $2m{s^{ - 2}}$ and hence we have
$\eqalign{
  & F - \left( {{m_1} + {m_2} + {m_3}} \right)g\sin \theta = \left( {{m_1} + {m_2} + {m_3}} \right)a \cr
  & \Rightarrow F = \left( {{m_1} + {m_2} + {m_3}} \right)g\sin \theta + \left( {{m_1} + {m_2} + {m_3}} \right)a \cr
  & \Rightarrow F = \left( {3 + 2 + 5} \right) \times 10 \times \sin 30 + \left( {3 + 2 + 5} \right)2 \cr
  & \Rightarrow F = 50N + 20N \cr
  & \therefore F = 70N \cr} $
Let ${N_{12}}$ be the normal reaction force between blocks 1 and 2 and ${N_{23}}$ be the normal reaction force between blocks 2 and 3. Between 1 and 2 we have
$\eqalign{
  & {N_{12}} - \left( {{m_2} + {m_3}} \right)g\sin \theta = \left( {{m_2} + {m_3}} \right)a \cr
  & \Rightarrow {N_{12}} - \left( {2 + 5} \right)g\sin 30 = \left( {2 + 5} \right) \times 2 \cr
  & \Rightarrow {N_{12}} = 35N + 14N \cr
  & \therefore {N_{12}} = 49N \cr} $
Similarly between 2 and 3 we have
$\eqalign{
  & {N_{23}} - \left( {{m_3}} \right)g\sin \theta = \left( {{m_3}} \right)a \cr
  & \Rightarrow {N_{23}} - \left( 5 \right)g\sin 30 = \left( 5 \right) \times 2 \cr
  & \Rightarrow {N_{23}} = 25N + 10N \cr
  & \therefore {N_{23}} = 35N \cr} $
So we had the force required as 70 Newton and the normal reaction between first and second block as 49 Newton and between second and third block as 35 Newton.

Note:
In the given question there is no frictional force between the blocks and the inclined. If there is frictional force then the answer would be different because friction force will oppose the motion of the blocks. Since the blocks are intended to move upwards the incline, friction will be acting downwards the incline.