Question

Three cubes on each side \[5cm\] are joined end to end. Find the surface area of the resultant cuboid.

Answer 1

Hint: The cubes are joined end to end , therefore the length of will be \[\left( {5 + 5 + 5} \right)cm = 15cm\] . The breadth and height of the resultant cuboid will remain the same as they are joined end to end . So, to find the surface area of the resultant cuboid we use formula \[S = 2\left( {l \times b + b \times h + l \times h} \right)\] , where \[l,b,h\] are length , breadth and height of the resultant cuboid respectively .

Complete step by step answer:
For better understanding we draw a figure representing the cubes joined end to end .

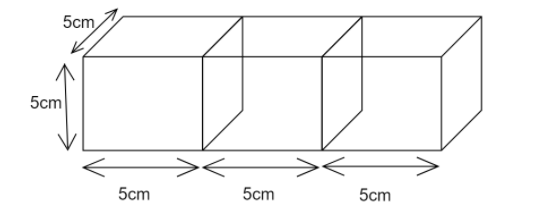
Now , for the resultant cuboid we have the following dimensions :
Length \[l = 15cm\]
Breadth \[b = 5cm\]
Height \[h = 5cm\]
Now , using the formula for Surface of a cuboid ,
\[S = 2\left( {l \times b + b \times h + l \times h} \right)\] ,
On putting the values we get ,
\[S = 2\left( {15 \times 5 + 5 \times 5 + 15 \times 5} \right)c{m^2}\]
On solving we get ,
\[S = 2\left( {75 + 25 + 75} \right)c{m^2}\]
On simplifying we get ,
\[S = \left( {2 \times 175} \right)c{m^2}\]
On solving we get ,
\[S = 350c{m^2}\] .
Therefore, the surface area of the resultant cuboid is \[350c{m^2}\].

Note:
Alternate Method :
In this method we will calculate the area of three cubes separately . So , the formula for surface area of the cube is \[6{l^2}\] , where \[l\] is the side of a cube . Now when three cubes are joined together the surface area of one face of the left and right cube from the end will not be calculated as it is merged with the middle cube . Now , the middle cube has two faces of which the surface area will not be calculated as it is merged with the other two as shown in figure .

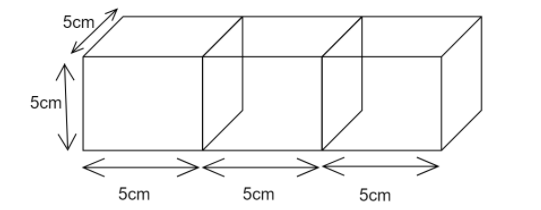
So , we have to calculate the area of \[5\] surfaces of the left cube , \[4\] surfaces of the middle cube and \[5\] surfaces of the right cube also . Therefore , total surface area will be
\[ = 5{l^2} + 4{l^2} + 5{l^2}\]
Putting the value of \[l\] as \[5\] , we get
\[ = \left[ {5{{\left( 5 \right)}^2} + 4{{\left( 5 \right)}^2} + 5{{\left( 5 \right)}^2}} \right]c{m^2}\]
On solving we get ,
\[\left( { = 5 \times 25 + 4 \times 25 + 5 \times 25} \right)c{m^2}\]
On simplifying we get
\[ = \left( {125 + 100 + 125} \right)c{m^2}\]
\[ = 350c{m^2}\]