
Three-person P, Q, and R of the same mass travel with the same speed $u$ along with an equilateral triangle of side \['d'\] such that each one faces the other always. After how much time will they meet each other?
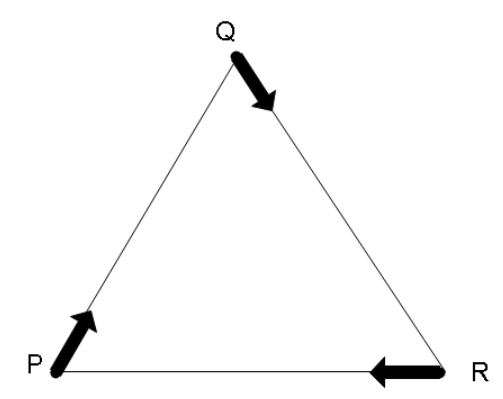
Answer
233.1k+ views
Hint: In this solution, we will use the concepts of relative velocity. We will consider a particular person and determine the time it will take for the person to reach the centre of the triangle where all three people will meet.
Complete step by step answer:
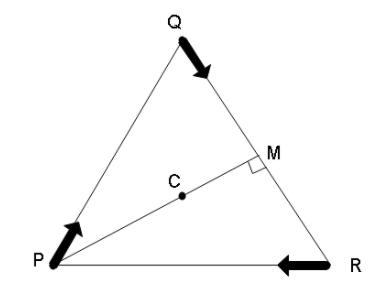
In the diagram given to us, we can see that tall the three persons will have a velocity direction such that they will always be facing each other. This implies that while the initial direction of velocities of all the 3 people is in the direction of the sides of the triangle but eventually the velocity vector will shift as all the three people start moving inwards.
This implies that all three people slowly moving inward will eventually meet at the centroid of the triangle. Now, the distance between, say person P, and the centroid will be $2/3$ times the length of the segment that joins P and the midpoint of the opposite side. SO, we can write
$PC = \dfrac{2}{3}PM$
Now, in an equilateral triangle, $PM \bot QR$, so using Pythagoras theorem, we can write
$P{M^2} + M{R^2} = P{R^2}$
We can solve this for $PM$ as
$P{M^2} = P{R^2} - M{R^2}$
Substituting the value of $PR = d$ and $MR = d/2$ (as M is the middle point), we get
$P{M^2} = {d^2} - {\left( {\dfrac{d}{2}} \right)^2}$
$P{M^2} = \dfrac{{3{d^2}}}{4}$
Which gives us
$PM = \dfrac{{\sqrt 3 d}}{2}$
So, we can find $PC = \dfrac{2}{3}PM$ as
$PC = \dfrac{2}{3} \times \dfrac{{\sqrt 3 d}}{2}$
$ \Rightarrow PC = d/\sqrt 3 $
So, the distance that has to be travelled by person P will be $a = d/\sqrt 3 $ and the velocity vector will have a component corresponding to the difference of the angle formed by the two lines which will be equal to $\theta = 60 + ( - 30) = 30^\circ $. This is the angle between the velocity vectors of two persons P and Q.
So, we can write the effective component of velocity will be $v = u\cos 30^\circ $
Then the time taken by persons to meet will be:
$t = \dfrac{{d/\sqrt 3 }}{{u\cos 30^\circ }}$
$\therefore t = \dfrac{{2d}}{{3u}}\,{\text{seconds}}$
Note: Here we should realize to use the concepts of relative velocity which will clarify our calculations very much. In doing so, we must be careful to take the distance to be travelled to be equal to the distance between one of the vertices of the triangle and the centroid. And while calculating the relative velocity, we must take the net component of the velocity taking into account the angle between the velocity vectors of two people.
Complete step by step answer:

In the diagram given to us, we can see that tall the three persons will have a velocity direction such that they will always be facing each other. This implies that while the initial direction of velocities of all the 3 people is in the direction of the sides of the triangle but eventually the velocity vector will shift as all the three people start moving inwards.
This implies that all three people slowly moving inward will eventually meet at the centroid of the triangle. Now, the distance between, say person P, and the centroid will be $2/3$ times the length of the segment that joins P and the midpoint of the opposite side. SO, we can write
$PC = \dfrac{2}{3}PM$
Now, in an equilateral triangle, $PM \bot QR$, so using Pythagoras theorem, we can write
$P{M^2} + M{R^2} = P{R^2}$
We can solve this for $PM$ as
$P{M^2} = P{R^2} - M{R^2}$
Substituting the value of $PR = d$ and $MR = d/2$ (as M is the middle point), we get
$P{M^2} = {d^2} - {\left( {\dfrac{d}{2}} \right)^2}$
$P{M^2} = \dfrac{{3{d^2}}}{4}$
Which gives us
$PM = \dfrac{{\sqrt 3 d}}{2}$
So, we can find $PC = \dfrac{2}{3}PM$ as
$PC = \dfrac{2}{3} \times \dfrac{{\sqrt 3 d}}{2}$
$ \Rightarrow PC = d/\sqrt 3 $
So, the distance that has to be travelled by person P will be $a = d/\sqrt 3 $ and the velocity vector will have a component corresponding to the difference of the angle formed by the two lines which will be equal to $\theta = 60 + ( - 30) = 30^\circ $. This is the angle between the velocity vectors of two persons P and Q.
So, we can write the effective component of velocity will be $v = u\cos 30^\circ $
Then the time taken by persons to meet will be:
$t = \dfrac{{d/\sqrt 3 }}{{u\cos 30^\circ }}$
$\therefore t = \dfrac{{2d}}{{3u}}\,{\text{seconds}}$
Note: Here we should realize to use the concepts of relative velocity which will clarify our calculations very much. In doing so, we must be careful to take the distance to be travelled to be equal to the distance between one of the vertices of the triangle and the centroid. And while calculating the relative velocity, we must take the net component of the velocity taking into account the angle between the velocity vectors of two people.
Recently Updated Pages
Dimensions of Charge: Dimensional Formula, Derivation, SI Units & Examples

How to Calculate Moment of Inertia: Step-by-Step Guide & Formulas

Circuit Switching vs Packet Switching: Key Differences Explained

Dimensions of Pressure in Physics: Formula, Derivation & SI Unit

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




