Question

Total power consumption for the given circuit is:

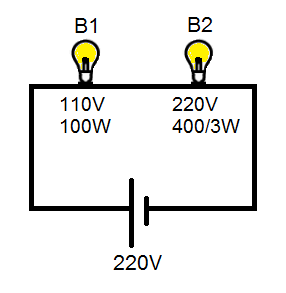
(A) $25\;W$
(B) $50\;W$
(C) $100\;W$
(D) $75\;W$

Answer 1

Hint To find the power consumption for the given circuit, first we calculate the individual resistances of each bulb then as the bulbs are connected in series, we can find the equivalent resistance of the complete circuit. Using equivalent resistance and the voltage of the complete circuit, power can be easily calculated.
Formula used:
$P = \dfrac{{{V^2}}}{R}$
Where P stands for the power, V stands for the voltage and R stands for the resistance.

Complete step by step answer
Let us first consider the ${B_1}$.
The voltage of the bulb ${B_1}$ is given as, ${V_1} = 110V$
Power of the bulb ${B_1}$ is given as, ${P_1} = 100W$
The resistance of the bulb ${B_1}$ can be calculated as, ${R_1} = \dfrac{{{V_1}^2}}{{{P_1}}}$
$ \Rightarrow {R_1} = \dfrac{{{{110}^2}}}{{100}}$
$ \Rightarrow {R_1} = \dfrac{{110 \times 110}}{{100}}$
$ \Rightarrow {R_1} = 121\Omega $
Now, let us consider the second bulb, ${B_2}$.
The voltage of the bulb ${B_2}$ is given as, ${V_2} = 220V$
Power of the bulb ${B_2}$ is given as, ${P_2} = \dfrac{{400}}{3}W$
The resistance of the bulb ${B_2}$ can be calculated as, ${R_2} = \dfrac{{{V_2}^2}}{{{P_2}}}$
$ \Rightarrow {R_2} = \dfrac{{{{220}^2}}}{{\dfrac{{400}}{3}}}$
$ \Rightarrow {R_2} = \dfrac{{220 \times 220 \times 3}}{{400}}$
$ \Rightarrow {R_2} = 363\Omega $
As we can see in the circuit, the bulbs ${B_1}$ and ${B_2}$ are connected in series.
So, the equivalent resistance of the circuit can be given as, ${R_{eq}} = {R_1} + {R_2}$
${R_{eq}} = (121 + 363)\Omega $
${R_{eq}} = 484\Omega $
The voltage of the complete circuit, $V = 220V$
Total power consumption for the given circuit, $P = \dfrac{{{V^2}}}{{{R_{eq}}}}$
$ \Rightarrow P = \dfrac{{{{220}^2}}}{{484}}$
$ \Rightarrow P = \dfrac{{220 \times 220}}{{484}}$
$ \Rightarrow P = 100W$
So, the total power consumption for the given circuit is $100\;W$.

Hence, The correct answer is option (C) $100\;W$.

Note There are two formulae to calculate the power of a given circuit:
1. $P = {I^2}R$, where I stands for the current and R stands for the resistance
2. $P = \dfrac{{{V^2}}}{R}$ , where V stands for the voltage and R stands for the resistance
We use these formulae depending on the quantities provided to us in the question. Here, the voltages of individual bulbs and also the voltage of the complete circuit are given to us, so we have used the second formula.