Question

How many transverse common tangents can be drawn?

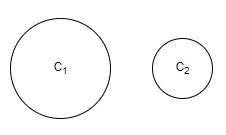
A. 1
B. 2
C. 3
D. 4

Answer 1

Hint: The tangents intersecting two circles are known as transverse common tangents. An example is given below:

Complete step-by-step answer:

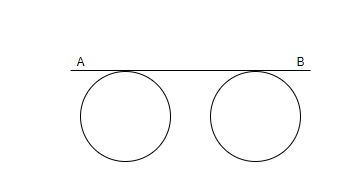
Here, AB is a transverse tangent to the two circles. Then we will apply various conditions and then come to a final conclusion.
We are given in the question that there are two circles $C_1$ and $C_2$ and then we have to find the number of transverse common tangents to the circles $C_1$ and $C_2$.

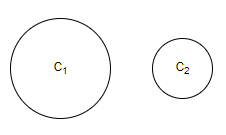
Please note that the number of tangents will depend on the relative positions of the given circles. We will get a different number of transverse common tangents in different situations. We know that, transverse common tangent is the tangent intersecting two circles. Now, we will see different types of situations based on the relative positions of the circles.
Condition 1: When one circle is lying completely inside the other circle.

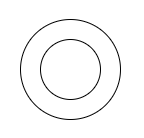
In this case, there is no common tangent possible because if any line touches the inner circle then it will cut the outer circle at two points but the tangent should have only one point in common. Also, if the tangent touches the outer circle, then it would not pass through the inner circle. So, we have no common transverse tangents in this case.
Condition 2: When the two circles touch each other internally.

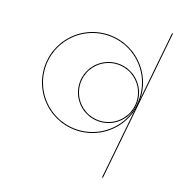
In this case, we have only one common tangent possible for the two circles.
Condition 3: When the two circles are intersecting each other at two points.

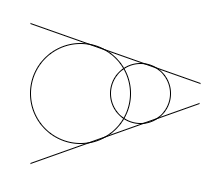
In this case, there are two common transverse tangents possible for the two circles.
Condition 4: When the two circles touch each other externally.

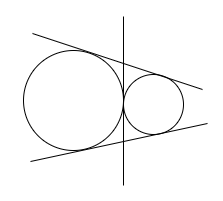
In this case, there are three common transverse tangents possible for the two circles.
Condition 5: When the two circles are separated by a distance and are not overlapping.

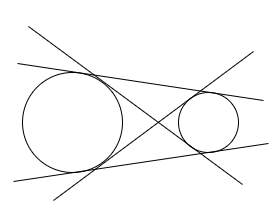
In this case, there are four common transverse tangents possible for the two circles.
Now in the question, we are given that the two circles, $C_1$ and $C_2$ are separated by a distance. Hence, on going through all the above discussed conditions, we can see that condition 5 matches our case. Hence, the number of common transverse tangents possible for the two circles, $C_1$ and $C_2$ is four.
Therefore, option (D) is the correct answer.

Note: We have to keep in mind that there are only five conditions possible for the position of two circles and the students can check each condition, and check which condition matches the figure given in the question in order to find the common transverse tangents.