
How many triangles can be formed by joining the vertices of a hexagon?
A. 31
B. 25
C. 20
D. 60
Answer
485.4k+ views
Hint: As we know that hexagon has \[6\] vertices means \[6\] points and the triangle has \[3\] points means a triangle need \[3\] vertices to be formed. Then, the numbers of triangles that can be formed by joining the vertices of a hexagon can be calculated by applying the concept of combination.
Complete step by step solution:
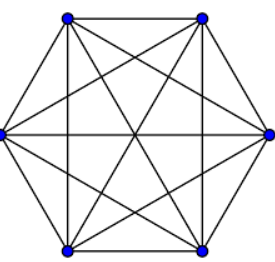
The number of vertices in a hexagon is \[6\].
The number of vertices in a triangle is \[3\].
That means to make a triangle we need \[3\] vertices.
So,\[6\]is the total number of vertices in hexagons, and out of those 6 vertices, 3 vertices that being chosen at a time to make a triangle.
By applying the formula of combination:
\[{}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}\] where, n is the total numbers of objects and r is the number of objects to be chosen as a time.
Therefore,
\[{}^6{C_3} = \dfrac{{6!}}{{3! \times \left( {6 - 3} \right)!}} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}}\]
By using the values of factorial terms:
We have, \[6!\] can be written as \[6 \times 5 \times 4 \times 3 \times 2 \times 1\] and \[3!\] can be written as \[3 \times 2 \times 1.\]
Replace \[6!\] = \[6 \times 5 \times 4 \times 3 \times 2 \times 1\] and \[3!\]= \[3 \times 2 \times 1\] in the following equation,
\[
{}^6{C_3} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}} \\
= \dfrac{{6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{3 \times 2 \times 1\left( {3 \times 2 \times 1} \right)}} = \dfrac{{120}}{6} = 20 \\
\]
$\therefore$ The number of triangles that can be formed by joining the vertices of a hexagon is \[20\]. Hence, option (C) is correct.
Note:
These types of questions always use a combination concept for solving the problem.
Some important definitions you should know
Vertices mean the point where \[2\] or more lines meet.
Combination: Any of the ways we can combine things when the order does not matter.
Combination formula: The formula of combination is \[{}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}\], where \[n\] represents the number of items and \[r\] represents the number of the items that being chosen at a time.
The factorial function\[(!)\]: The factorial function means to multiply all whole numbers from the chosen numbers down to \[1\].
The representation of factorial is \[n!\].
Alternatively, you can draw the figure and count the triangles but it becomes complicated.
Complete step by step solution:

The number of vertices in a hexagon is \[6\].
The number of vertices in a triangle is \[3\].
That means to make a triangle we need \[3\] vertices.
So,\[6\]is the total number of vertices in hexagons, and out of those 6 vertices, 3 vertices that being chosen at a time to make a triangle.
By applying the formula of combination:
\[{}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}\] where, n is the total numbers of objects and r is the number of objects to be chosen as a time.
Therefore,
\[{}^6{C_3} = \dfrac{{6!}}{{3! \times \left( {6 - 3} \right)!}} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}}\]
By using the values of factorial terms:
We have, \[6!\] can be written as \[6 \times 5 \times 4 \times 3 \times 2 \times 1\] and \[3!\] can be written as \[3 \times 2 \times 1.\]
Replace \[6!\] = \[6 \times 5 \times 4 \times 3 \times 2 \times 1\] and \[3!\]= \[3 \times 2 \times 1\] in the following equation,
\[
{}^6{C_3} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}} \\
= \dfrac{{6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{3 \times 2 \times 1\left( {3 \times 2 \times 1} \right)}} = \dfrac{{120}}{6} = 20 \\
\]
$\therefore$ The number of triangles that can be formed by joining the vertices of a hexagon is \[20\]. Hence, option (C) is correct.
Note:
These types of questions always use a combination concept for solving the problem.
Some important definitions you should know
Vertices mean the point where \[2\] or more lines meet.
Combination: Any of the ways we can combine things when the order does not matter.
Combination formula: The formula of combination is \[{}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}\], where \[n\] represents the number of items and \[r\] represents the number of the items that being chosen at a time.
The factorial function\[(!)\]: The factorial function means to multiply all whole numbers from the chosen numbers down to \[1\].
The representation of factorial is \[n!\].
Alternatively, you can draw the figure and count the triangles but it becomes complicated.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

Trending doubts
What are the elders in Goa nostalgic about class 11 social science CBSE

Formaldehyde at room temperature is ALiquid BGas CSolid class 11 chemistry CBSE

Define least count of vernier callipers How do you class 11 physics CBSE

Distinguish between Mitosis and Meiosis class 11 biology CBSE

Why are forests affected by wars class 11 social science CBSE

Explain zero factorial class 11 maths CBSE




