Question

Two adjacent sides of a parallelogram are 10 cm and 12 cm. If one of the diagonals is 16 cm long, find the area of the parallelogram. Also find distance between its shorter sides.
(a) $119.8c{{m}^{2}};11.98cm$
(b) $119.9c{{m}^{2}};11.20cm$
(c) $117.6c{{m}^{2}};10.28cm$
(d) $120.8c{{m}^{2}};15.98cm$

Answer 1

Hint: Find the area of the parallelogram by dividing it in two equal triangles. Since the length of one diagonal is given to us we can find out the area of a triangle with sides 16 cm, 10 cm and 12 cm. Multiply the area of the triangle by 2 to get the area of parallelogram. Then use the formula that the area of a parallelogram is base multiplied by the height to find the distance between the shorter sides. Use the shorter side as base and the distance will be the height.

Complete step-by-step answer:
In this problem the length of two adjacent sides of parallelogram are given to us. Which are 10 cm and 12 cm. Let us draw the parallelogram first.

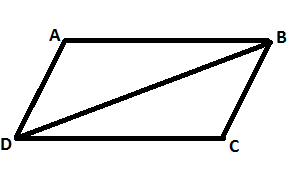
Here ABCD is the parallelogram. AB = CD = 12 cm and AD = BC = 10 cm.
The length of the diagonal BD is also given to us. BD = 16 cm.

We need to find out the area of parallelogram ABCD. If we can find the area of triangle BCD then we will also get the area of ABCD by multiplying the area of triangle BCD by 2. As three sides of triangle BCD and triangle BAD have the same lengths, also the areas will be the same for both the triangles.
For triangle BCD, the length of the sides are BC = 10 cm, CD = 12 cm, BD =16 cm. Therefore, the semi perimeter will be:
$s=\dfrac{BC+CD+BD}{2}$
$\Rightarrow s=\dfrac{10+12+16}{2}=19$

Hence, the area of the triangle BCD is:
$\sqrt{s\left( s-BC \right)\left( s-CD \right)\left( s-BD \right)}$
 $=\sqrt{19\times \left( 19-10 \right)\times \left( 19-12 \right)\times \left( 19-16 \right)}$
$=\sqrt{19\times 9\times 7\times 3}$
$=\sqrt{3591}=59.9c{{m}^{2}}$
Therefore, the area of the parallelogram will be,
$2\times 59.92=119.8c{{m}^{2}}$
We know that the area of a parallelogram = $base\times height$.

If we take the shorter side as our base then the height will be the distance between the shorter sides. Therefore,
$10\times height=119.8$
$\Rightarrow height=\dfrac{119.8}{10}$
$\Rightarrow height=11.98$
Therefore the distance between the shorter sides is 11.98 cm.
Hence, option (a) is correct.

Note: Since it is a multiple choice question, to solve it very quickly we can just use the fact that the area of a parallelogram = $base\times height$, where the base is 10. Now if we look at the options very carefully, only option (a) is satisfying the condition. Therefore option (a) is correct.