Question

Two circles of radii 5cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.

Answer 1

Hint:
we will first prove that the line joining the centers of the two circles and the common chord are perpendicular to each other and also prove that the line joining the centers of the two circles bisect the common chord by using congruent triangle and then we will apply the Pythagorean Theorem to find the length of common chord.

Complete step by step solution:

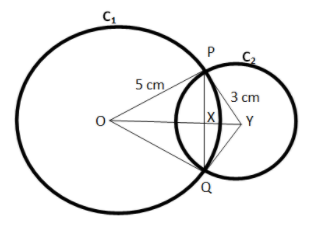
Let the two circles be C1 with centre O and C2 with centre Y. PQ is the required common chord which intersects OY at X.
Given that:
$\begin{array}{rl}& \Rightarrow OP=5cm\\ & \Rightarrow YP=3cm\end{array}$
In $△OPYand△OQY$
$\Rightarrow OP=OQ$ (radius of circle C1)
$\Rightarrow PY=QY$ (radius of circle C2)
$\Rightarrow OY=OY$ (common)
$\therefore △OPY\cong OQY$ (SSS congruence rule)
$\Rightarrow \mathrm{\angle }POY=\mathrm{\angle }QOY$ (C.P.C.T) …………………..
Now,
In $△POXand△QOX$
$\Rightarrow OP=OQ$ (radius of circle C1)
$\Rightarrow \mathrm{\angle }POX=\mathrm{\angle }QOX$( from (1) )
$\Rightarrow OX=OX$ (common)
$\therefore △POX\cong QOX$(SAS congruence rule)
$\Rightarrow \mathrm{\angle }PXO=\mathrm{\angle }QXO$ (C.P.C.T) ……………………
$\left(2\right)$
$\mathrm{\&}PX=QX$ (C.P.C.T) ……………………………. $\left(3\right)$
Since PQ is a straight line. So,
$\Rightarrow \mathrm{\angle }PXO+\mathrm{\angle }QXO={180}^o$
$\Rightarrow \mathrm{\angle }PXO+\mathrm{\angle }PXO={180}^o$ ( From)
$\Rightarrow 2\mathrm{\angle }PXO={180}^o$
$\Rightarrow \mathrm{\angle }PXO={90}^o$
$\Rightarrow \therefore \mathrm{\angle }PXO=\mathrm{\angle }QXO={90}^o$
Therefore,
$△PXO\text{ and }△PXY$ is a right angled triangle.
Let $OX=xsoXY=4-x$
Using Pythagoras Theorem in ;
$\begin{array}{rl}& \Rightarrow \text{In }△PXO\\ & \Rightarrow O{P}^2=O{X}^2+P{X}^2\\ & \Rightarrow 5^2=x^2+P{X}^2\\ & \Rightarrow 5^2-x^2=P{X}^2\end{array}$ ………………$\left(4\right)$
$\begin{array}{rl}& \Rightarrow \text{In }△PXY\\ & \Rightarrow P{Y}^2=X{Y}^2+P{X}^2\\ & \Rightarrow 3^2={(4-x)}^2+P{X}^2\\ & \Rightarrow 3^2-{(4-x)}^2=P{X}^2\end{array}$ ………………$\left(5\right)$

Equating $\left(4\right)$and$\left(5\right)$, we get;
$\begin{array}{rl}& 3^2-{(4-x)}^2=5^2-x^2\\ & 9-(16+x^2-8x)=25-x^2\end{array}$
$\Rightarrow 8x=32$
$\Rightarrow x={\displaystyle \frac{32}{8}}$
$\Rightarrow x=4$
Putting value of x in equation $\left(4\right)$, we get;
$\Rightarrow P{X}^2=5^2-4^2$
$\begin{array}{rl}& \Rightarrow PX=\sqrt{25-16}\\ & \Rightarrow PX=\sqrt{9}\end{array}$
$\therefore PX=3cm$
So required length of common chord
$\Rightarrow =PX+QX$
$=PX+PX$ (From equation )
$\begin{array}{rl}& \Rightarrow 2PX\\ & \Rightarrow 2\times 3cm\end{array}$
$=6cm$

Note:
A chord of a circle is defined as the straight line segment whose endpoints lie on a circle. Also, a chord that passes through the centre of a circle is called a diameter and it is the longest chord of a circle.