Question

Two circles touch each other externally. The sum of their areas is $130\pi c{{m}^{2}}$ and the distance between their centres is 14 cm. Find the diameters of the circles (in cm).
(a) 22, 8
(b) 22, 6
(c) 26, 8
(d) 22, 4

Answer 1

Hint: We start solving the problem by assuming the radii of the two circles and drawing the figure representing the given information. We then use the fact that the distance between the centres of two externally touching circles is equal to the sum of the radii of those two circles for our first condition given in the problem. We then use the fact that the area of the circle is $\pi {{r}^{2}}$ for the second condition given in the problem. We then solve both these conditions to get the radii of the circles. We then use the fact that diameter is twice the radius of the circles to get the required answer.

Complete step-by-step answer:
According to the problem, we are given that two circles touch each other externally in which the sum of their area is $130\pi c{{m}^{2}}$ and distance between their centres is 14 cm. We need to find the diameters of the circles (in cm).
Let us assume the radii of the circles are ${{r}_{1}}$ and ${{r}_{2}}$. Let us draw the figure representing the given information.

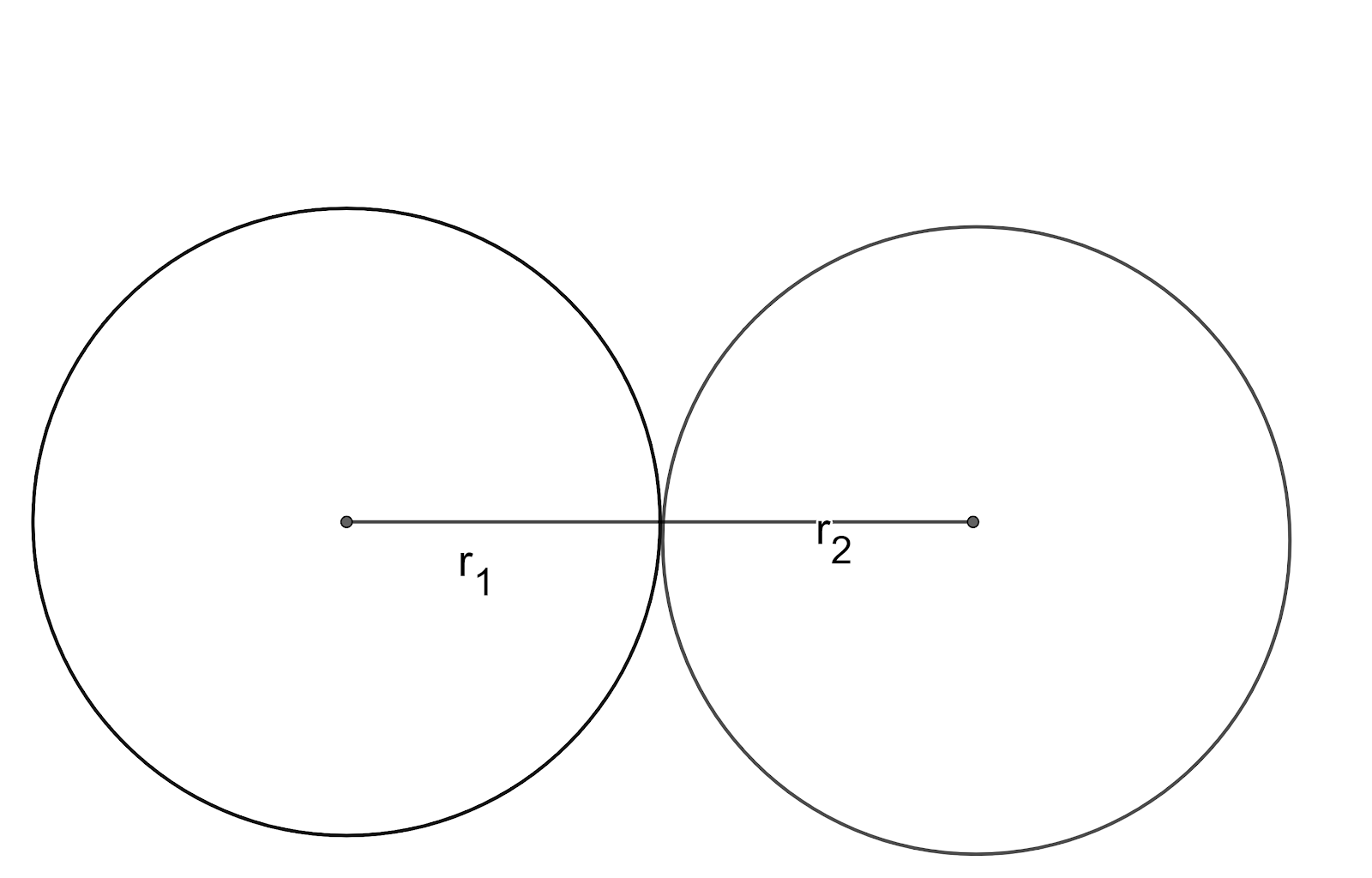
We know that the distance between the centres of two externally touching circles is equal to the sum of the radii of those two circles.
So, we get ${{r}_{1}}+{{r}_{2}}=14cm$.
$\Rightarrow {{r}_{1}}=14-{{r}_{2}}$ ---(1).
We know that the area of the circles is defined as $\pi {{r}^{2}}$, where r is the radius of the circle.
From the problem, we have $\pi r_{1}^{2}+\pi r_{2}^{2}=130\pi $.
From equation (1), we get
$\Rightarrow \pi {{\left( 14-{{r}_{2}} \right)}^{2}}+\pi r_{2}^{2}=130\pi $.
\[\Rightarrow 196-28{{r}_{2}}+r_{2}^{2}+r_{2}^{2}=130\].
\[\Rightarrow 2r_{2}^{2}-28{{r}_{2}}+66=0\].
\[\Rightarrow r_{2}^{2}-14{{r}_{2}}+33=0\].
Using the factorisation method, we have
\[\Rightarrow r_{2}^{2}-11{{r}_{2}}-3{{r}_{2}}+33=0\].
\[\Rightarrow {{r}_{2}}\left( {{r}_{2}}-11 \right)-3\left( {{r}_{2}}-11 \right)=0\].
\[\Rightarrow \left( {{r}_{2}}-3 \right)\left( {{r}_{2}}-11 \right)=0\].
\[\Rightarrow {{r}_{2}}-3=0\] or \[{{r}_{2}}-11=0\].
\[\Rightarrow {{r}_{2}}=3\] or \[{{r}_{2}}=11\].
If \[{{r}_{2}}=3\], then \[{{r}_{1}}=14-3=11\].
If \[{{r}_{2}}=11\], then \[{{r}_{1}}=14-11=3\].
So, the radii of the circles are 11, 3 cm. We know that the diameter of the circle is twice the radius of that circle.
So, we get the diameters of the circles as 22, 6 cm.
The correct options for the given problem is (b).

So, the correct answer is “Option (b)”.

Note: We should not stop solving the problem after finding the radii of the circles as we are asked to find the diameters of the circles. We can also use the area of the circle as $\dfrac{\pi {{d}^{2}}}{4}$, where d is the diameter of the circle to solve this problem. But this may take a few more steps to get the required answer. We can also find the area of each circle individually using the obtained diameter of each circle. Similarly, we can expect problems to find the perimeters of both circles.