Question

Two consecutive angles of a parallelogram are in ratio 1:6, then which of the following is the smaller angle:
A. $\dfrac{1080}{7}$
B. $\dfrac{180}{7}$
C. $\dfrac{540}{7}$
D. None of these

Answer 1

Hint: We are given that the two consecutive angles of a parallelogram are in ratio 1:6. Let us consider x to be one angle, that is, $\angle ABC\text{ }$ of a parallelogram ABCD. Then, the other angle will be $\angle BCD=6x$ which is obtained from the ratio $\dfrac{\angle ABC}{\angle BCD}=\dfrac{1}{6}$ . We know that the sum of two consecutive angles of a parallelogram is ${{180}^{{}^\circ }}$ . Hence, $x+6x={{180}^{{}^\circ }}$ . Now, we have to solve this equation to get the value of x and substitute in $\angle BCD=6x$ to find the other angle.

Complete step-by-step answer:
We are given that the two consecutive angles of a parallelogram are in ratio 1:6. Let us consider a parallelogram ABCD as shown below.

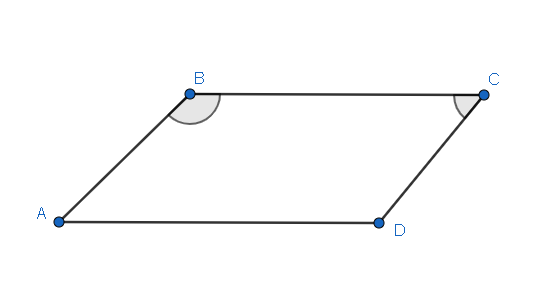
Let us consider $\angle ABC\text{ and }\angle BCD\text{ }$ . These angles are in the ratio 1:6.
$\Rightarrow \dfrac{\angle ABC}{\angle BCD}=\dfrac{1}{6}$
Let us assume $\angle ABC=x\text{ }$ . Then
$\begin{align}
  & \dfrac{x}{\angle BCD}=\dfrac{1}{6} \\
 & \Rightarrow \angle BCD=6x \\
\end{align}$
We know that the sum of two consecutive angles of a parallelogram is ${{180}^{{}^\circ }}$ . Hence,
$x+6x={{180}^{{}^\circ }}$
On adding the terms in LHS, we will get
\[\begin{align}
  & 7x={{180}^{{}^\circ }} \\
 & \Rightarrow x={{\left( \dfrac{180}{7} \right)}^{{}^\circ }} \\
\end{align}\]
Now, let’s find $\angle BCD$.
$\angle BCD=6\times \dfrac{180}{7}={{\left( \dfrac{1080}{7} \right)}^{{}^\circ }}$
Hence, the smallest angle is \[{{\left( \dfrac{180}{7} \right)}^{{}^\circ }}\] .
Hence, the correct option is B.

So, the correct answer is “Option B”.

Note: You need not find $\angle BCD$ as it is six times $\angle ABC$ and will be certainly greater than $\angle ABC$ . You may make a mistake by writing the sum of two consecutive angles of a parallelogram as ${{90}^{{}^\circ }}$ . You must know the theorems associated with parallelograms to solve this question.