
Two fair dice are rolled. Then the probability of getting a composite number as the sum of the face values is equal to
A. $\dfrac{7}{12}$
B. $\dfrac{5}{12}$
C. $\dfrac{1}{12}$
D. $\dfrac{3}{4}$
E. $\dfrac{2}{3}$
Answer
586.8k+ views
Hint: To solve this question, we should know about the sample space and the favourable cases for the required event. The sample space when two dice are rolled is given by $S=\left\{ \left( 1,1 \right)\left( 1,2 \right)\left( 1,3 \right)......\left( 6,4 \right)\left( 6,5 \right)\left( 6,6 \right) \right\}$ where the elements in the ordered pair are the numbers appeared on the two dice. We can write that the total number of elements in the sample space is $n\left( S \right)=6\times 6=36$. We should write the favourable cases out of the sample space whose sum is a composite number and the probability is given by ${{p}_{required}}=\dfrac{n\left( favorable \right)}{n\left( S \right)}$.
Complete step by step answer:
We are given a sample space that has two dice. When two dice are rolled, the sample space is as follows
$S=\left\{ \left( 1,1 \right)\left( 1,2 \right)\left( 1,3 \right)......\left( 6,4 \right)\left( 6,5 \right)\left( 6,6 \right) \right\}$ where $\left( x,y \right)$ denotes that the first dice is rolled the number-x and the second dice is rolled the number-y.
There are 6 possibilities each for the first dice and second dice. So, the total number of elements is given by $n\left( S \right)=6\times 6=36$
The value of the sum ranges from 2 to 12.
Let us consider the sum of the two numbers is S and an event E which has the value of S as a composite number.
The favorable cases for the event E are
$S=4,6,8,9,10,12$ as these are the composite numbers in the range of the sum.
Let us consider $S=4$. The ordered pairs for which we get the sum as 4 are
$\left( 1,3 \right),\left( 3,1 \right),\left( 2,2 \right)$
So, $N\left( S=4 \right)=3$
Let us consider $S=6$. The ordered pairs for which we get the sum as 4 are
$\left( 1,5 \right),\left( 5,1 \right),\left( 2,4 \right),\left( 4,2 \right)\left( 3,3 \right)$
So, $N\left( S=6 \right)=5$
Let us consider $S=8$. The ordered pairs for which we get the sum as 4 are
$\left( 2,6 \right),\left( 6,2 \right),\left( 3,5 \right),\left( 5,3 \right),\left( 4,4 \right)$
So, $N\left( S=8 \right)=5$
Let us consider $S=9$. The ordered pairs for which we get the sum as 4 are
$\left( 3,6 \right),\left( 6,3 \right),\left( 4,5 \right),\left( 5,4 \right)$
So, $N\left( S=9 \right)=4$
Let us consider $S=10$. The ordered pairs for which we get the sum as 4 are
$\left( 4,6 \right),\left( 6,4 \right),\left( 5,5 \right)$
So, $N\left( S=10 \right)=3$
Let us consider $S=12$. The ordered pairs for which we get the sum as 4 are
$\left( 6,6 \right)$
So, $N\left( S=12 \right)=1$
We can write that
$\begin{align}
& N\left( E \right)=N\left( S=4 \right)+N\left( S=6 \right)+N\left( S=8 \right)+N\left( S=9 \right)+N\left( S=10 \right)+N\left( S=12 \right) \\
& N\left( E \right)=3+5+5+4+3+1=21 \\
\end{align}$
We can write the required probability as
$P\left( E \right)=\dfrac{N\left( E \right)}{N\left( S \right)}=\dfrac{21}{36}=\dfrac{7}{12}$
$\therefore $The required probability is $\dfrac{7}{12}$. The answer is option-A.
Note:
There is a shortcut to get the number of ordered pairs for the sum when two dice are rolled. The below figure has the sum as the x-axis and the number of ordered pairs on the y-axis. The number starts at 1 for the sum=2 and increases one by one until it reaches the value of 6 at sum=7. Again, it decreases one by one to reach the value of 1 when sum=12. Using this method, we can easily write the number of ordered pairs instead of writing the ordered pairs for every question.
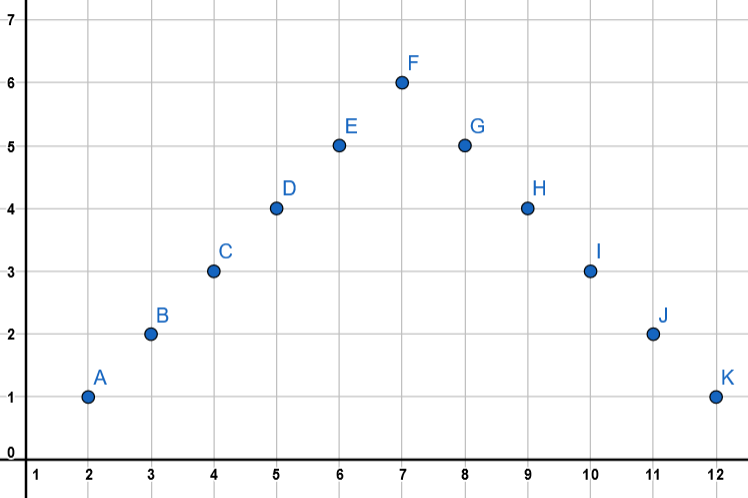
Complete step by step answer:
We are given a sample space that has two dice. When two dice are rolled, the sample space is as follows
$S=\left\{ \left( 1,1 \right)\left( 1,2 \right)\left( 1,3 \right)......\left( 6,4 \right)\left( 6,5 \right)\left( 6,6 \right) \right\}$ where $\left( x,y \right)$ denotes that the first dice is rolled the number-x and the second dice is rolled the number-y.
There are 6 possibilities each for the first dice and second dice. So, the total number of elements is given by $n\left( S \right)=6\times 6=36$
The value of the sum ranges from 2 to 12.
Let us consider the sum of the two numbers is S and an event E which has the value of S as a composite number.
The favorable cases for the event E are
$S=4,6,8,9,10,12$ as these are the composite numbers in the range of the sum.
Let us consider $S=4$. The ordered pairs for which we get the sum as 4 are
$\left( 1,3 \right),\left( 3,1 \right),\left( 2,2 \right)$
So, $N\left( S=4 \right)=3$
Let us consider $S=6$. The ordered pairs for which we get the sum as 4 are
$\left( 1,5 \right),\left( 5,1 \right),\left( 2,4 \right),\left( 4,2 \right)\left( 3,3 \right)$
So, $N\left( S=6 \right)=5$
Let us consider $S=8$. The ordered pairs for which we get the sum as 4 are
$\left( 2,6 \right),\left( 6,2 \right),\left( 3,5 \right),\left( 5,3 \right),\left( 4,4 \right)$
So, $N\left( S=8 \right)=5$
Let us consider $S=9$. The ordered pairs for which we get the sum as 4 are
$\left( 3,6 \right),\left( 6,3 \right),\left( 4,5 \right),\left( 5,4 \right)$
So, $N\left( S=9 \right)=4$
Let us consider $S=10$. The ordered pairs for which we get the sum as 4 are
$\left( 4,6 \right),\left( 6,4 \right),\left( 5,5 \right)$
So, $N\left( S=10 \right)=3$
Let us consider $S=12$. The ordered pairs for which we get the sum as 4 are
$\left( 6,6 \right)$
So, $N\left( S=12 \right)=1$
We can write that
$\begin{align}
& N\left( E \right)=N\left( S=4 \right)+N\left( S=6 \right)+N\left( S=8 \right)+N\left( S=9 \right)+N\left( S=10 \right)+N\left( S=12 \right) \\
& N\left( E \right)=3+5+5+4+3+1=21 \\
\end{align}$
We can write the required probability as
$P\left( E \right)=\dfrac{N\left( E \right)}{N\left( S \right)}=\dfrac{21}{36}=\dfrac{7}{12}$
$\therefore $The required probability is $\dfrac{7}{12}$. The answer is option-A.
Note:
There is a shortcut to get the number of ordered pairs for the sum when two dice are rolled. The below figure has the sum as the x-axis and the number of ordered pairs on the y-axis. The number starts at 1 for the sum=2 and increases one by one until it reaches the value of 6 at sum=7. Again, it decreases one by one to reach the value of 1 when sum=12. Using this method, we can easily write the number of ordered pairs instead of writing the ordered pairs for every question.

Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




